Giải Bài 40 trang 81 sách bài tập toán 7 - Cánh diều
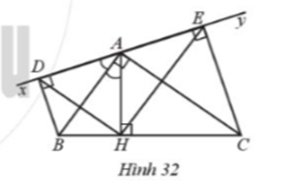
Cho Hình 32 có (widehat {BAC} = 90^circ ), AH vuông góc với BC tại H, (widehat {xAB} = widehat {BAH}) , Ay là tia đối của tia Ax. BD và CE vuông góc với xy lần lượt tại D và E. Chứng minh:
Đề bài
Cho Hình 32 có \(\widehat {BAC} = 90^\circ \) , AH vuông góc với BC tại H, \(\widehat {xAB} = \widehat {BAH}\) , Ay là tia đối của tia Ax. BD và CE vuông góc với xy lần lượt tại D và E. Chứng minh:
a) AC là tia phân giác của góc Hay;
b) BD + CE = BC;
c) DH vuông góc với HE.
Phương pháp giải - Xem chi tiết
- Chứng minh \(\widehat {CAH} = \widehat {CAy}\) suy ra AC là tía phân giác của \(\widehat {HAy}\).
- Chứng minh: ∆ABD = ∆ABH (cạnh huyền – góc nhọn) suy ra BD = BA
Tương tự chứng minh: CH = CE
Từ đó: BC = BH + CH
Mà BD = BH, CE = CH.
Do đó BC = BD + CE.
- Gọi I là giao điểm của AB và DH
Chứng minh ∆ADI = ∆AHI (c.g.c) suy ra \(\widehat {ADI} = \widehat {AHI}\)
Tương tự chứng minh: \(\widehat {AHE} = \widehat {AEH}\)
Tính số đo góc HDE bằng \({90^o}\) nên DH vuông góc với HE
Lời giải chi tiết
a) •Ta có \(\widehat {xAy} = \widehat {xAB} + \widehat {BAC} + \widehat {CAy}\)
Hay \(180^\circ = \widehat {xAB} + 90^\circ + \widehat {CAy}\)
Suy ra \(\widehat {CAy} = 90^\circ - \widehat {xAB}\)
•Ta có \(\widehat {BAH} + \widehat {CAH} = \widehat {BAC} = 90^\circ \)
Nên \(\widehat {CAH} = 90^\circ - \widehat {BAH}\)
Mà \(\widehat {xAB} = \widehat {BAH}\) (giả thiết)
Suy ra \(\widehat {CAH} = \widehat {CAy}\)
Do đó AC là tia phân giác của \(\widehat {HAy}\)
Vậy AC là tia phân giác của \(\widehat {HAy}\) .
b) • Xét ∆ABD và ∆ABH có:
\(\widehat {ADB} = \widehat {AHB}\left( { = 90^\circ } \right)\)
AB là cạnh chung,
\(\widehat {DAB} = \widehat {HAB}\) (giả thiết),
Do đó ∆ABD = ∆ABH (cạnh huyền – góc nhọn).
Suy ra BD = BH , AD = AH (các cặp cạnh tương ứng).
• Xét ∆ACE và ∆ACH có:
\(\widehat {AEC} = \widehat {AHC}\left( { = 90^\circ } \right)\)
AC là cạnh chung,
\(\widehat {CAH} = \widehat {CAE}\) (chứng minh câu a),
Do đó ∆ACE = ∆ACH (cạnh huyền – góc nhọn).
Suy ra CE = CH, AE = AH (các cặp cạnh tương ứng).
•Ta có BC = BH + CH
Mà BD = BH, CE = CH.
Do đó BC = BD + CE.
Vậy BC = BD + CE.
c) Gọi I là giao điểm của AB và DH, K là giao điểm của EH và AC.
• Xét ∆ADI và ∆AHI có:
AD = AH (chứng minh câu b),
\(\widehat {DAI} = \widehat {HAI}\) (do \(\widehat {xAB} = \widehat {BAH}\)),
AI là cạnh chung.
Do đó ∆ADI = ∆AHI (c.g.c).
Suy ra \(\widehat {ADI} = \widehat {AHI}\) (hai góc tương ứng).
Hay \(\widehat {ADH} = \widehat {AHD}\).
• Xét ∆AHK và ∆AEK có:
AH = AE (chứng minh câu b),
\(\widehat {HAK} = \widehat {EAK}\) (do \(\widehat {HAC} = \widehat {EAC}\)),
AK là cạnh chung
Do đó ∆AHK = ∆AEK (c.g.c)
Suy ra \(\widehat {AHK} = \widehat {AEK}\) (hai góc tương ứng).
Hay \(\widehat {AHE} = \widehat {AEH}\).
Xét ∆ADH có: \(\widehat {ADH} + \widehat {AHD} + \widehat {HAD} = 180^\circ \) (tổng ba góc của một tam giác).
Mà \(\widehat {ADH} = \widehat {AHD}\) nên \(\widehat {AHD} = \frac{{180^\circ - \widehat {HAD}}}{2}\)
Xét ∆AEH có: \(\widehat {AEH} + \widehat {AHE} + \widehat {HAE} = 180^\circ \) (tổng ba góc của một tam giác)
Mà \(\widehat {AHE} = \widehat {AEH}\) nên \(\widehat {AHE} = \frac{{180^\circ - \widehat {HAE}}}{2}\)
Ta có
\(\widehat {DHE} = \widehat {AHD} + \widehat {AHE} = \frac{{180^\circ - \widehat {HAD}}}{2} + \frac{{180^\circ - \widehat {HAE}}}{2} = \frac{{{{360}^o} - \left( {\widehat {HA{\rm{D}}} + \widehat {HA{\rm{E}}}} \right)}}{2} = \frac{{{{360}^o} - {{180}^o}}}{2} = {90^o}\)
Suy ra DH vuông góc với HE.
Vậy DH vuông góc với HE.