Giải bài 4.26 trang 18 sách bài tập toán 12 - Kết nối tri thức
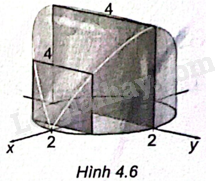
Tính thể tích vật thể B, biết đáy của B là hình tròn bán kính 2 và các mặt cắt vuông góc với mặt đáy là những hình vuông (H.4.6).
Đề bài
Tính thể tích vật thể B , biết đáy của B là hình tròn bán kính 2 và các mặt cắt vuông góc với mặt đáy là những hình vuông (H.4.6).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích \(V = \int\limits_a^b {S\left( x \right)dx} \). Trong đó vật thể giới hạn bởi hai mặt phẳng vuông góc với \(Ox\) tại điểm có hoành độ \(x = a,x = b\); mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) với \(x \in \left[ {a;b} \right]\) có thiết diện \(S\left( x \right)\). Từ giả thiết, xác định các thành phần trong công thức để tìm thể tích.
Lời giải chi tiết
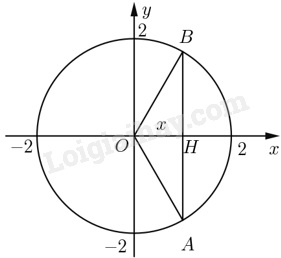
Ta có vật thể được giới hạn bởi hai mặt phẳng vuông góc với \(Ox\) tại điểm có hoành độ \(x = 2,x = - 2\) và mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) với \(x \in \left[ { - 2;2} \right]\) cắt vật thể theo thiết diện là hình vuông có độ dài cạnh là \(AB = 2 \cdot \sqrt {{2^2} - {x^2}} = 2\sqrt {4 - {x^2}} \).
Khi đó diện tích mặt cắt là \({\left( {2\sqrt {4 - {x^2}} } \right)^2} = 4\left( {4 - {x^2}} \right)\).
Suy ra thể tích vật thể là \(V = \int\limits_{ - 2}^2 {4\left( {4 - {x^2}} \right)dx} = \left. {\left( {16x - \frac{{4{x^3}}}{3}} \right)} \right|_{ - 2}^2 = 32 - \frac{{32}}{3} + 32 - \frac{{32}}{3} = \frac{{128}}{3}\).