Giải bài 4. 24 trang 17 sách bài tập toán 12 - Kết nối tri thức — Không quảng cáo

Đề bài

Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh $Ox$:

a) $y = 2\sqrt x ,{\rm{ y}} = 0,{\rm{ }}x = 1,{\rm{ }}x = 4$;

b) $y = 4x,{\rm{ }}y = {x^3},{\rm{ }}x = 0,{\rm{ }}x = 2$.

Lời giải chi tiết

a) Thể tích cần tìm là $V = \pi \int\limits_1^4 {{{\left( {2\sqrt x } \right)}^2}dx}  = \pi \int\limits_1^4 {4xdx}  = 2\pi \left. {{x^2}} \right|_1^4 = 32\pi  - 2\pi  = 30\pi$.

b) Ta có hình vẽ biểu hình phẳng cần tính diện tích như bên dưới.

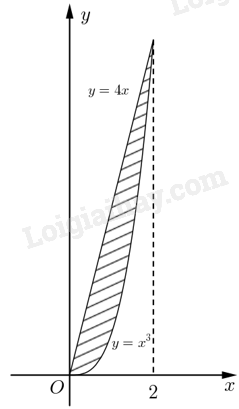
Ta thấy đồ thị của hàm số $y = 4x$ nằm phía trên đồ thị $y = {x^3}$. Do đó thể tích cần tìm sẽ bằng thể tích khối tròn

xoay khi quay hình phẳng giới hạn bởi các đường $y = 4x,{\rm{ }}y = 0,{\rm{ }}x = 0,{\rm{ }}x = 2$ quanh trục Ox (gọi là ${V_1}$ ) trừ đi thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường $y = {x^3},{\rm{ }}y = 0,{\rm{ }}x = 0,{\rm{ }}x = 2$ quanh trục Ox (gọi là ${V_2}$).

Ta có ${V_1} = \pi \int\limits_0^2 {{{\left( {4x} \right)}^2}dx}$ và ${V_2} = \pi \int\limits_0^2 {{{\left( {{x^3}} \right)}^2}dx}$.

Do đó thể tích cần tìm là

$V = {V_1} - {V_2} = \pi \int\limits_0^2 {{{\left( {4x} \right)}^2}dx}  - \pi \int\limits_0^2 {{{\left( {{x^3}} \right)}^2}dx}  = \pi \int\limits_0^2 {\left( {16{x^2} - {x^6}} \right)dx}$$= \pi \left. {\left( {\frac{{16}}{3}{x^3} - \frac{{{x^7}}}{7}} \right)} \right|_0^2 = \frac{{512\pi }}{{21}}$.