Giải bài 4.30 trang 86 SGK Toán 7 tập 1 - Kết nối tri thức
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM. Chứng minh rằng:
Đề bài
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM.
Chứng minh rằng:
a) \(\Delta \)OAN = \(\Delta \)OBM;
b) \(\Delta \)AMN = \(\Delta \)BNM.
Phương pháp giải - Xem chi tiết
Chứng minh 2 tam giác bằng nhau theo trường hợp cạnh-góc-cạnh.
Lời giải chi tiết
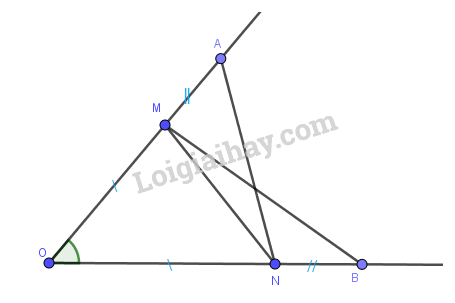
a) Xét \(\Delta OAN\) và \(\Delta OBM \) có:
OA=OB (gt)
\(\widehat{O}\) chung
OM=ON (gt)
=>\(\Delta OAN = \Delta OBM\)(c.g.c)
b) Do \(\Delta OAN = \Delta OBM\) nên AN=BM ( 2 cạnh tương ứng); \(\widehat {OAN} = \widehat {OBM}\)( 2 góc tương ứng) =>\(\widehat {NAM} = \widehat {MBN}\)
Do OA + AM = OM; OB + BN = ON
Mà OA = OB, OM =ON
=> AM=BN
Xét \(\Delta AMN\) và \(\Delta BNM\) có:
AN=BM (cmt)
\(\widehat {NAM} = \widehat {MBN}\) (cmt)
AM=BN (cmt)
=>\(\Delta AMN = \Delta BNM\)(c.g.c)