Giải bài 4.36 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức
Trong Hình 4.78, ta có AN = BM,
Đề bài
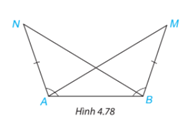
Trong Hình 4.78, ta có AN = BM,\(\widehat {BAN} = \widehat {ABM}\). Chứng minh rằng\(\widehat {BAM} = \widehat {ABN}\).
Phương pháp giải - Xem chi tiết
Chứng minh 2 tam giác ANB và BMA bằng nhau từ đó suy ra \(\widehat {BAM} = \widehat {ABN}\).
Lời giải chi tiết
Xét \(\Delta ANB \) và \(\Delta BMA\) có:
AN=BM (gt)
\(\widehat {BAN} = \widehat {ABM}\) (gt)
AB chung
=>\(\Delta ANB = \Delta BMA\)(c.g.c)
=> \(\widehat{ABN} = \widehat{BAM}\) (2 góc tương ứng)
Cùng chủ đề:
Giải bài 4. 36 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức