Giải bài 4.37 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.
Đề bài
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.
Phương pháp giải - Xem chi tiết
Hình thoi là tứ giác có 4 cạnh của tứ giác bằng nhau.
Lời giải chi tiết
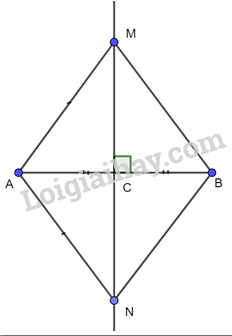
Vì M, N nằm trên đường trung trực của AB nên MA = MB ; NA = NB ( tính chất)
Mà MA = NA (gt)
Do đó, MA = NA = MB = NB.
Xét tam giác AMB và tam giác ANB có:
MA = NA (gt)
MB = NB (cmt)
AB chung
Do đó, ∆AMB = ∆ANB (c – c – c).
\(\Rightarrow \widehat{AMB}=\widehat{ANB}\) (2 góc tương ứng).
Vậy MB = NB và góc AMB bằng góc ANB.
Cùng chủ đề:
Giải bài 4. 37 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức