Giải bài 4.37 trang 66 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
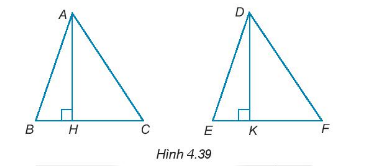
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng
Đề bài
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng
a) Nếu AB = DE, BC = EF và AH = DK thì \(\Delta ABC = \Delta DEF;\)
b) Nếu AB = DE, AC = DF và AH = DK thì \(\Delta ABC = \Delta DEF\)
Phương pháp giải - Xem chi tiết
a)
-Chứng minh \(\Delta HAB = \Delta KDE\left( {ch - cgv} \right)\)
-Chứng minh \(\Delta ABC = \Delta DEF\left( {c - g - c} \right)\)
b)
-Chứng minh \(HB = KE;HC = KF \Rightarrow BC = EF\)
Lời giải chi tiết
a)
Xét \(\Delta HAB\) và \(\Delta KDE\) có:
\(\widehat H = \widehat K = {90^0}\\HA = KD\left( {gt} \right)\\AB = DE\left( {gt} \right)\\ \Rightarrow \Delta HAB = \Delta KDE\left( {ch - cgv} \right)\)
\(\Rightarrow \widehat {ABH} = \widehat {DEK}\) ( 2 góc tương ứng) hay \(\widehat {ABC} = \widehat {DEF}\)
Xét \(\Delta ABC\) và \(\Delta DEF\) có:
\(\begin{array}{l}BA = ED\\BC = EF\\\widehat {ABC} = \widehat {DEF}\\ \Rightarrow \Delta ABC = \Delta DEF\left( {c - g - c} \right)\end{array}\)
b)
Chứng minh tương tự như trên có các cặp tam giác vuông bằng nhau:
\(\Delta HAB = \Delta KDE;\Delta HAC = \Delta KDF\)
\( \Rightarrow HB = KE;HC = KF\) (cặp cạnh tương ứng)
Ta có:
\(\left\{ \begin{array}{l}BC = HB + HC\\EF = KE + KF\end{array} \right. \Rightarrow BC = EF\)
Xét \(\Delta ABC\) và \(\Delta DEF\) có:
\(\begin{array}{l}AB = DE\left( {gt} \right)\\AC = DF\left( {gt} \right)\\BC = EF\left( {cmt} \right)\\ \Rightarrow \Delta ABC = \Delta DEF\left( {c - c - c} \right)\end{array}\)