Giải bài 4 (4.15) trang 65 vở thực hành Toán 7
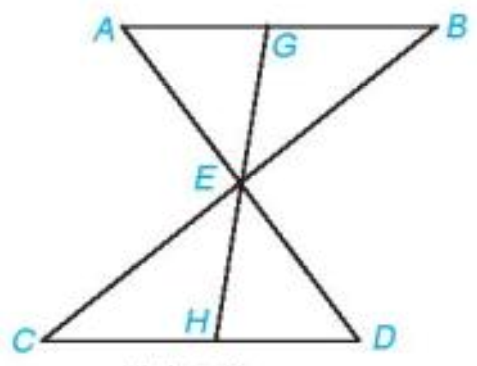
Bài 4 (4.15). Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như hình dưới đây. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G,H,E thẳng hàng Chứng minh rằng a) \(\Delta ABE = \Delta DCE\) b) EG = EH.
Đề bài
Bài 4 (4.15). Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như hình dưới đây. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G,H,E thẳng hàng Chứng minh rằng
a) \(\Delta ABE = \Delta DCE\)
b) EG = EH.
Phương pháp giải - Xem chi tiết
Chứng minh hai tam giác bằng nhau theo trường hợp 3.
Lời giải chi tiết
a) \(\Delta ABE\) và \(\Delta DCE\) có
\(\widehat {ABE} = \widehat {ECD}\)(hai góc so le trong)
AB = CD (theo giả thiết)
\(\widehat {BAE} = \widehat {EDC}\)(hai góc so le trong)
Do đó \(\Delta ABE = \Delta DCE\left( {g.c.g} \right)\)
b) \(\Delta AGE\) và \(\Delta DHE\) có
\(\widehat {GAE} = \widehat {EDH}\)(hai góc so le trong)
AE = ED (\(\Delta ABE = \Delta DCE\))
\(\widehat {GEA} = \widehat {HED}\)(hai góc đối đỉnh)
Do đó \(\Delta AGE = \Delta DHE\left( {g.c.g} \right)\). Từ đây suy ra EG = EH