Giải bài 4 trang 115 SGK Toán 7 tập 2 - Cánh diều — Không quảng cáo

Đề bài

Tam giác ABC có ba đường phân giác cắt nhau tại I . Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC . Chứng minh tam giác ABC đều.

Lời giải chi tiết

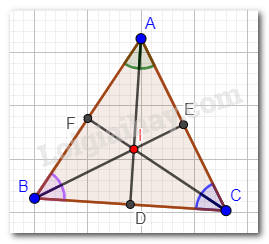
Ta có: I là giao điểm của ba đường phân giác của tam giác ABC . Đồng thời là giao điểm của ba đường trung trực tam giác ABC nên: \(ID \bot BC;IE \bot AC;IF \bot AB\).

Xét tam giác ADB và tam giác ADC có:

\(\widehat {BAD} = \widehat {CAD}\)( AD là phân giác của góc A );

AD chung;

\(\widehat {ADB} = \widehat {ADC}(=90^0)\)(vì \(ID \bot BC\)).

Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)

Tương tự ta có: \(\Delta BEA = \Delta BEC\)(g.c.g). Suy ra: BA = BC ( 2 cạnh tương ứng) . (2)

Từ (1) và (2) suy ra: AB = BC = AC .

Vậy tam giác ABC đều.