Giải bài 4 trang 107 SGK Toán 7 tập 2 - Cánh diều
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:
Đề bài
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G . Gọi H là hình chiếu của A lên đường thẳng BC . Giả sử H là trung điểm của đoạn thẳng BM . Chứng minh:
a) \(\Delta AHB = \Delta AHM\); b) \(AG = \dfrac{2}{3}AB\).
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta AHB = \Delta AHM\) theo trường hợp c.g.c.
b) Dựa vào kết quả chứng minh phần a) và tính chất ba đường trung tuyến trong tam giác để chứng minh.
Lời giải chi tiết
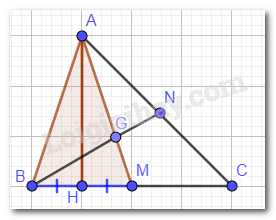
a) Xét tam giác AHB và tam giác AHM có:
AH chung;
\(\widehat {AHB} = \widehat {AHM}\)( H là hình chiếu của A lên BC nên \(AH \bot BC\));
HB = HM ( H là trung điểm của BM ).
Vậy \(\Delta AHB = \Delta AHM\)(c.g.c).
b) \(\Delta AHB = \Delta AHM\)nên AB = AM ( 2 cạnh tương ứng) .
G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC . Nên: \(AG = \dfrac{2}{3}AM\).
Mà AB = AM suy ra: \(AG = \dfrac{2}{3}AB\).