Giải bài 4 trang 80 SGK Toán 8 tập 1– Chân trời sáng tạo
Cho hình bình hành
Đề bài
Cho hình bình hành \(ABCD\) ( \(AB > BC\) ). Tia phân giác của góc \(D\) cắt \(AB\) tại \(E\) , tia phân giác của góc \(B\) cắt \(CD\) tại \(F\)
a) Chứng minh \(DE\) // \(BF\)
b) Tứ giác \(DEBF\) là hình gì?
Phương pháp giải - Xem chi tiết
a) Chỉ ra cặp góc đồng vị bằng nhau
b) Áp dụng dấu hiệu nhận biết hình bình hành
Lời giải chi tiết
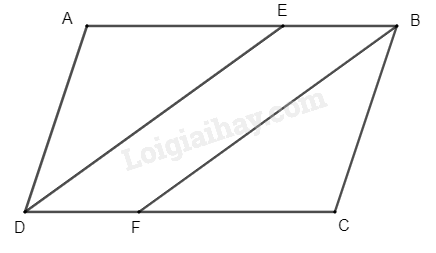
a) Vì \(DE\) , \(BF\) là phân giác (gt)
Suy ra \(\widehat {{\rm{ADE}}} = \widehat {{\rm{EDC}}} = \frac{{\widehat {ADC}}}{2}\) ; \(\widehat {{\rm{EBF}}} = \widehat {{\rm{CBF}}} = \frac{{\widehat {ABC}}}{2}\) (1)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AB\) // \(CD\) và \(\widehat {ADC} = \widehat {ABC}\) (2)
Suy ra \(\widehat {{\rm{AED}}} = \widehat {{\rm{EDC}}}\) (so le trong) (3)
Từ (1), (2), (3) suy ra \(\widehat {AED} = \widehat {ABF}\)
Mà hai góc ở vị trí đồng vị
Suy ra \(DE\) // \(BF\)
b) Xét tứ giác \(DEBF\) ta có:
\(DE\) // \(BF\) (cmt)
\(BE\) // \(DF\) (do \(AB\) // \(CD\) )
Suy ra \(DEBF\) là hình bình hành