Giải bài 42 trang 121 sách bài tập toán 9 - Cánh diều tập 1
Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A sao cho \(\widehat {MAP} = 60^\circ \) (Hình 46). Tìm độ dài của dây Curoa mắc qua hai ròng rọc theo a.
Đề bài
Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A sao cho \(\widehat {MAP} = 60^\circ \) (Hình 46). Tìm độ dài của dây Curoa mắc qua hai ròng rọc theo a.
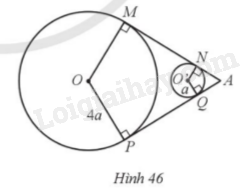
Phương pháp giải - Xem chi tiết
Độ dài dây curoa = độ dài cung lớn MP + độ dài cung nhỏ NQ + MN + PQ
Bước 1: Áp dụng lý thuyết về tổng 4 góc trong tứ giác để tính số đo góc MOP và góc NO’Q, từ đó suy ra số đo cung lớn MP và cung nhỏ NQ.
Bước 2: Áp dụng công thức \(l = \frac{{\pi Rn}}{{180}}\) để tính độ dài 2 cung trên.
Bước 3: Chứng minh \(MN = PQ\), tính \(MN = AM - AN = OM.\cot \widehat {OAM} - O'N.\cot \widehat {OAM}\).
Lời giải chi tiết
Do AM, AP là tiếp tuyến của (O) nên \(MA = PA\) và \(OM \bot MA,OP \bot PA\), do đó \(\widehat M = \widehat P = 90^\circ \) và AO là tia phân giác của góc MAP nên \(\widehat {MAO} = \widehat {PAO} = \frac{{\widehat {MAP}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \)
Do AN, AQ là tiếp tuyến của (O’) nên \(NA = QA\) và \(O'N \bot NA,O'Q \bot QA\), do đó \(\widehat {O'NA} = \widehat {O'QA} = 90^\circ \) và AO’ là tia phân giác của góc NAQ nên \(\widehat {NAO'} = \widehat {QAO'} = \frac{{\widehat {NAQ}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \)
Xét tứ giác OMAP có \(\widehat {MOP} + \widehat M + \widehat {MAP} + \widehat P = 360^\circ \) nên \(\widehat {MOP} = 360^\circ - \left( {\widehat M + \widehat {MAP} + \widehat P} \right)\)\( = 360^\circ - \left( {90^\circ + 60^\circ + 90^\circ } \right) = 120^\circ \), suy ra số đo cung nhỏ MP là 120⁰
Số đo cung lớn MP là \(360^\circ - 120^\circ = 240^\circ \) và có độ dài là \({l_1} = \frac{{\pi .4a.240}}{{180}} = \frac{{16\pi a}}{3}\)
Xét tứ giác O’NAQ có \(\widehat {NO'Q} + \widehat {O'NA} + \widehat {O'QA} + \widehat {NAQ} = 360^\circ \) nên \(\widehat {NO'Q} = 360^\circ - \left( {\widehat {O'NA} + \widehat {O'QA} + \widehat {NAQ}} \right)\) \( = 360^\circ - \left( {90^\circ + 90^\circ + 60^\circ } \right) = 120^\circ \), suy ra số đo cung nhỏ NQ là 120⁰ và có độ dài là \({l_2} = \frac{{\pi .a.120}}{{180}} = \frac{{2\pi a}}{3}\)
Ta có: \(MN = MA - NA;PQ = PA - QA\), mà \(MA = PA;NA = QA\) suy ra \(MN = PQ\).
Xét tam giác OAM vuông tại M có:
\(MA = OM.\cot \widehat {OAM} = a.\cot 30^\circ = 4a\sqrt 3 \).
Xét tam giác O’AN vuông tại N có:
\(NA = ON.\cot O'AN = a.\cot 30^\circ = a\sqrt 3 \).
Ta có: \(MN = PQ = MA - NA = 4a\sqrt 3 - a\sqrt 3 = 3\sqrt 3 a\)
Độ dài dây Curoa mắc qua 2 ròng rọc là:
\(\frac{{16\pi a}}{3} + \frac{{2\pi a}}{3} + 3\sqrt 3 a + 3\sqrt 3 a = 6a\left( {\pi + \sqrt 3 } \right)\).