Giải bài 44 trang 45 sách bài tập toán 11 - Cánh diều
Lập bảng biến thiên và vẽ đồ thị hàm số:
Đề bài
Lập bảng biến thiên và vẽ đồ thị hàm số:
a) \(y = {\left( {\sqrt 2 } \right)^x};\)
b) \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^x};\)
c) \(y = {\log _{\sqrt 3 }}x;\)
d) \(y = - {\log _2}x.\)
Phương pháp giải - Xem chi tiết
Sử dụng các tính chất của lũy thừa với số mũ hữu tỉ để rút gọn biểu thức.
Lời giải chi tiết
a) Vì hàm số \(y = {\left( {\sqrt 2 } \right)^x}\) có cơ số \(\sqrt 2 > 1\) nên ta có bảng biến thiên như sau:
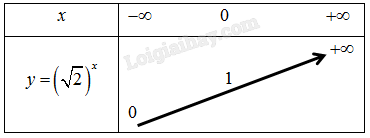
Đồ thị của hàm số \(y = {\left( {\sqrt 2 } \right)^x}\) là một đường cong liền nét đi qua các điểm \(\left( { - 2;\frac{1}{2}} \right),\left( {0;1} \right),\left( {2;2} \right),\left( {4;4} \right).\)
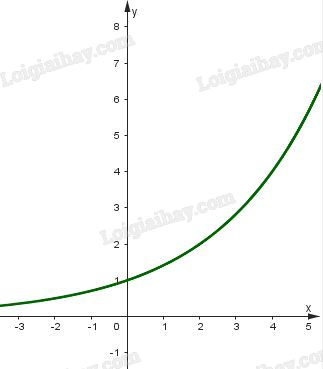
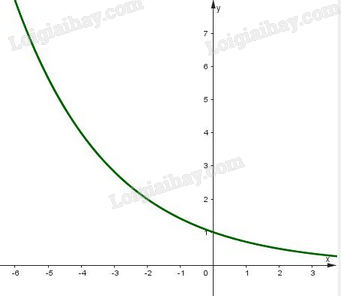
b) Vì hàm số \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^x}\) có cơ số \(\frac{1}{{\sqrt 2 }} < 1\) nên ta có bảng biến thiên như sau:
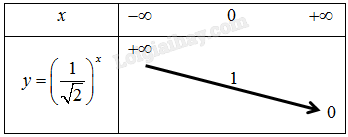
Đồ thị của hàm số \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^x}\) là một đường cong liền nét đi qua các điểm \(\left( { - 4;4} \right),\left( { - 2;2} \right),\left( {0;1} \right),\left( {2;\frac{1}{2}} \right).\)
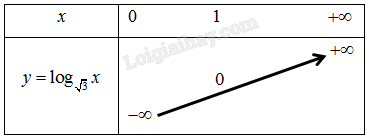
c) Vì hàm số \(y = {\log _{\sqrt 3 }}x\) có cơ số \[\sqrt 3 > 1\] nên ta có bảng biến thiên như sau:
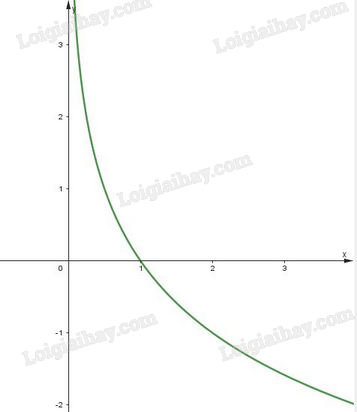
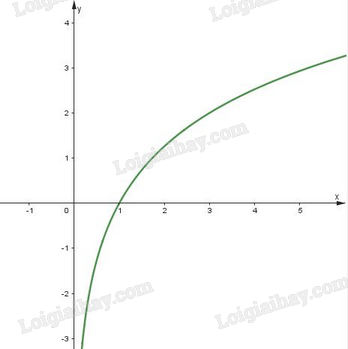
Đồ thị của hàm số \(y = {\log _{\sqrt 3 }}x\) là một đường cong liền nét đi qua các điểm \(\left( {\frac{1}{3}; - 2} \right),\left( {1;0} \right),\left( {3;2} \right),\left( {9;4} \right).\)
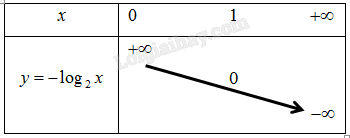
d) Vì hàm số \(y = - {\log _2}x\) có cơ số \(2 > 1\) nên ta có bảng biến thiên như sau:
Đồ thị của hàm số \(y = - {\log _2}x\) là một đường cong liền nét đi qua các điểm \(\left( {\frac{1}{2};1} \right),\left( {1;0} \right),\left( {2; - 1} \right),\left( {4; - 2} \right).\)