Giải bài 48 trang 110 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho hình chóp $S.ABCD$ có $ABCD$ là hình chữ nhật, $AB = 2a$, $AD = 3a$, tam giác $\left( {SAB} \right)$ vuông cân tại $S$ và nằm trong mặt phẳng vuông góc với $\left( {ABCD} \right)$. Tính khoảng cách:

a) Từ điểm $C$ đến mặt phẳng $\left( {SAB} \right)$.

b) Giữa hai đường thẳng $SB$ và $CD$.

c) Giữa hai đường thẳng $BC$ và $SA$.

d) Từ điểm $S$ đến mặt phẳng $\left( {ABCD} \right)$.

Lời giải chi tiết

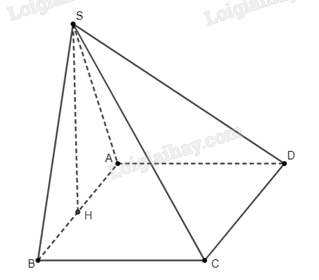
a) Gọi $H$ là trung điểm của $AB$. Do tam giác $SAB$ vuông cân tại $S$ nên ta có $SA \bot SB$ và $SH \bot AB$. Hơn nữa, do $\left( {SAB} \right) \bot \left( {ABCD} \right)$ và $AB$ là giao tuyến của 2 mặt phẳng đó, ta suy ra $SH \bot \left( {ABCD} \right)$. Từ đó $SH \bot BC$.

Do $ABCD$ là hình chữ nhật, ta suy ra $AB \bot BC$. Như vậy, do $SH \bot BC$, $AB \bot BC$ ta suy ra $\left( {SAB} \right) \bot BC$. Như vậy $B$ là hình chiếu của $C$ trên mặt phẳng $\left( {SAB} \right)$, từ đó khoảng cách cần tính là đoạn thẳng $BC$. Mà $BC = 3a$, nên khoảng cách từ điểm $C$ đến $\left( {SAB} \right)$ là $3a$.

b) Do $ABCD$ là hình chữ nhật, ta suy ra $CD\parallel AB$, mà $AB \subset \left( {SAB} \right)$ nên $CD\parallel \left( {SAB} \right)$. Hơn nữa, do $SB \subset \left( {SBC} \right)$, nên khoảng cách giữa hai đường thẳng $SB$ và $CD$ cũng chính là khoảng cách giữa $CD$ và $\left( {SBC} \right)$, và nó cũng bằng khoảng cách từ điểm $C$ đến $\left( {SBC} \right)$. Theo câu a, khoảng cách này chính là đoạn thẳng $BC$, tức là khoảng cách giữa hai đường thẳng $SB$ và $CD$ bằng $3a$.

c) Theo câu a, ta có $SA \bot SB$. Hơn nữa, ta cũng có $\left( {SAB} \right) \bot BC$ nên $SB \bot BC$. Như vậy, $SB$ là đường vuông góc chung của 2 đường thẳng $SA$ và $BC$, điều này có nghĩa khoảng cách giữa $SA$ và $BC$ là đoạn thẳng $SB$.

Tam giác $SAB$ vuông cân tại $S$ nên ta có $A{B^2} = 2S{B^2} \Rightarrow SB = \frac{{AB}}{{\sqrt 2 }}$

Mà $AB = 2a$ nên $SB = \frac{{2a}}{{\sqrt 2 }} = a\sqrt 2$.

Vậy khoảng cách giữa $SA$ và $BC$ là $a\sqrt 2$.

d) Theo câu a, ta có $SH \bot \left( {ABCD} \right)$. Điều này có nghĩa khoảng cách từ $S$ đến $\left( {ABCD} \right)$ là đoạn thẳng $SH$.

Tam giác $SAB$ vuông cân tại $S$ có đường trung tuyến $SH$ nên ta có $SH = \frac{{AB}}{2} = \frac{{2a}}{2} = a$.

Vậy khoảng cách từ $S$ đến $\left( {ABCD} \right)$ là $a$.