Giải Bài 49 trang 83 sách bài tập toán 7 - Cánh diều — Không quảng cáo

Đề bài

Cho Hình 37 có AB = AC = BC = BD = CE, \(\widehat {ABD} = \widehat {ACE} = 90^\circ \)

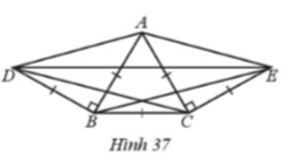
a) Chứng minh tam giác AED là tam giác cân.

b) Tính số đo các góc của tam giác ADE.

c) Chứng minh DC = BE

Lời giải chi tiết

a) Xét ∆ABD và ∆ACE có:

\(\widehat {ABD} = \widehat {ACE} = 90^\circ \) (giả thiết),

AB = AC (giả thiết),

BD = CE (giả thiết).

Do đó ∆ABD = ∆ACE (hai cạnh góc vuông)

Suy ra AD = AE (hai cạnh tương ứng).

Nên tam giác AED cân tại A.

Vậy tam giác AED cân tại A.

b) • Vì AB = AC = BC (giả thiết) nên tam giác ABC đều.

Suy ra \(\widehat {ABC} = \widehat {ACB} = \widehat {BAC} = 60^\circ \).

Vì AC = CE , \(\widehat {ACE} = 90^\circ \) (giả thiết) nên tam giác ACE vuông cân tại C.

Suy ra \(\widehat {CEA} = \widehat {CAE} = \frac{{180^\circ  - 90^\circ }}{2} = 45^\circ \)

Vì AB = BD , \(\widehat {ABD} = 90^\circ \) (giả thiết) nên tam giác ABD vuông cân tại B.

Suy ra \(\widehat {BAD} = \widehat {BDA} = \frac{{180^\circ  - 90^\circ }}{2} = 45^\circ \)

Ta có \(\widehat {DAE} = \widehat {DAB} + \widehat {BAC} + \widehat {CAE} = 45^\circ  + 60^\circ  + 45^\circ  = 150^\circ \)

• Vì tam giác AED cân tại A nên \(\widehat {ADE} = \widehat {AED}\)

Xét ∆ADE có: \(\widehat {ADE} + \widehat {AED} + \widehat {DAE} = 180^\circ \) (tổng ba góc của một tam giác)

Mà \(\widehat {EAD} = 150^\circ \), \(\widehat {ADE} = \widehat {AED}\)

Suy ra \(\widehat {ADE} = \widehat {AED} = \frac{{180^\circ  - 150^\circ }}{2} = 15^\circ \)

Vậy ∆ADE có \(\widehat {ADE} = \widehat {AED} = 15^\circ ,\widehat {EAD} = 150^\circ \)

c) Ta có \(\widehat {DBC} = \widehat {ABC} + \widehat {ABD} = 60^\circ  + 90^\circ  = 150^\circ \) ; \(\widehat {BCE} = \widehat {ACB} + \widehat {ACE} = 60^\circ  + 90^\circ  = 150^\circ \)

Xét ∆CBD và ∆BCE có:

BC là cạnh chung,

\(\widehat {B{\rm{D}}C} = \widehat {BCE}\) (cùng bằng 150°),

BD = CE (giả thiết),

Do đó ∆BDC = ∆CEB (c.g.c).

Suy ra DC = EB (hai cạnh tương ứng)

Vậy DC = BE.