Giải bài 5 trang 24 Chuyên đề học tập Toán 11 Cánh diều
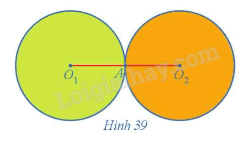
Cho hai đường tròn (O1; R) và (O2; R) tiếp xúc ngoài với nhau tại A (Hình 39).
Đề bài
Cho hai đường tròn (O 1 ; R) và (O 2 ; R) tiếp xúc ngoài với nhau tại A ( Hình 39 ).
a) Tìm phép tịnh tiến biến đường tròn (O 1 ) thành đường tròn (O 2 ).
b) Tìm phép đối xứng tâm biến đường tròn (O 1 ) thành đường tròn (O 2 ).
c) Tìm phép đối xứng trục biến đường tròn (O 1 ) thành đường tròn (O 2 ).
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức:
- Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.
- Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \({Đ_d}\).
Lời giải chi tiết
a) Hai đường tròn \(({O_1};{\rm{ }}R)\) và \(({O_2};{\rm{ }}R)\) có cùng bán kính. Ta có phép tịnh tiến theo vectơ \(\overrightarrow {{O_1}{O_2}} \) biến điểm tâm \({O_1}\) thành tâm \({O_2}\).
Như vậy, phép tịnh tiến theo vectơ \(\overrightarrow {{O_1}{O_2}} \) biến đường tròn \(({O_1};{\rm{ }}R)\)thành đường tròn \(({O_2};{\rm{ }}R)\)
b) Ta có: \({O_1}A{\rm{ }} = {\rm{ }}{O_2}A{\rm{ }} = {\rm{ }}R\) nên A là trung điểm của \({O_1}{O_2}\). Do đó, có phép đối xứng tâm A biến O 1 thành O 2 .
Như vậy, phép đối xứng tâm O biến đường tròn \(({O_1};{\rm{ }}R)\) thành đường tròn \(({O_2};{\rm{ }}R)\).
c)
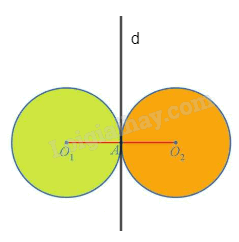
Qua A, kẻ đường thẳng d vuông góc với \({O_1}{O_2}.\)Khi đó đường thẳng d là đường trung trực của đoạn thẳng O 1 O 2 . Do đó, ta có phép đối xứng trục d biến O 1 thành O 2 .
Như vậy, phép đối xứng trục d biến đường tròn \(({O_1};{\rm{ }}R)\) thành đường tròn \(({O_2};{\rm{ }}R)\).