Giải bài 57 trang 29 sách bài tập toán 12 - Cánh diều
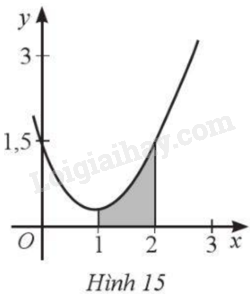
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S). Cho đồ thị hàm số (y = fleft( x right)) và gọi (S) là diện tích hình phẳng được tô màu như Hình 15. a) (S = intlimits_1^2 {fleft( x right)dx} ). b) (S = intlimits_0^{1,5} {left| {fleft( x right)} right|dx} ). c) (S = intlimits_0^{1,5} {fleft( x right)dx} ). d) (S = intlimits_1^2 {left| {fleft( x right)} right|dx} ).
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
Cho đồ thị hàm số \(y = f\left( x \right)\) và gọi \(S\) là diện tích hình phẳng được tô màu như Hình 15 .
a) \(S = \int\limits_1^2 {f\left( x \right)dx} \).
b) \(S = \int\limits_0^{1,5} {\left| {f\left( x \right)} \right|dx} \).
c) \(S = \int\limits_0^{1,5} {f\left( x \right)dx} \).
d) \(S = \int\limits_1^2 {\left| {f\left( x \right)} \right|dx} \).
Phương pháp giải - Xem chi tiết
Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết
Hình phẳng đã cho được giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = 1,x = 2\).
Diện tích hình phẳng được tính theo công thức:
\(S = \int\limits_1^3 {\left| {f\left( x \right)} \right|dx} = \int\limits_1^2 {f\left( x \right)dx} \) (vì \(f\left( x \right) > 0,\forall x \in \left[ {1;2} \right]\)).
Vậy a) đúng, b) sai, c) sai, d) đúng.
a) Đ.
b) S.
c) S.
d) Đ.