Giải bài 6. 41 trang 77 SGK Toán 8 - Cùng khám phá — Không quảng cáo

Đề bài

Cho $\Delta ABC$ có $AB = 9cm,AC = 12cm$ và $BC = 15cm.$ Trên cạnh $AB$ lấy điểm $M$ sao cho $AM = 4cm$ và trên cạnh $AB$ lấy điểm $N$ sao cho $AN = 3cm$ . Gọi $O$ là giao điểm của $CM$ và $BN$ . Chứng minh rằng:

a) $\Delta ABN ∽ \Delta ACM;$

b) $\Delta BMO ∽ \Delta CNO;$

c) $\Delta BOC ∽ \Delta MON;$

d) $CM$ là tia phân giác của góc $ACB$ và $\Delta MBN$ cân tại $M.$

Lời giải chi tiết

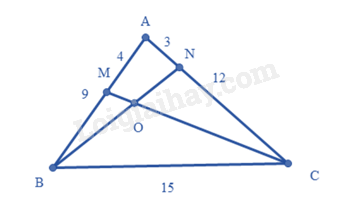
a) Xét hai tam giác $ABN$ và tam giác $ACM$ , ta có:

$\frac{{AB}}{{AC}} = \frac{{AN}}{{AM}} = \frac{3}{4}$

$\widehat A$ là góc chung

=> $\Delta ABN$ ∽ $\Delta ACM$ (cạnh-góc-cạnh)

b) Xét hai tam giác $BMO$ và tam giác $CNO$ , ta có:

$\widehat {MBO} = \widehat {NCO}$ (do $\Delta ABN$ ∽ $\Delta ACM$ )

$\widehat {MOB} = \widehat {NOC}$ (hai góc đối đỉnh)

=> $\Delta BMO$ ∽ $\Delta CNO$ (góc-góc)

c) Vì $\Delta BMO$ ∽ $\Delta CNO$ , ta có tỉ số đồng dạng:

$\frac{{OB}}{{OC}} = \frac{{MO}}{{NO}} \Rightarrow \frac{{OB}}{{NO}} = \frac{{OC}}{{NO}}$

Xét tam giác $BOC$ và tam giác $MON$ , ta có:

$\frac{{OB}}{{NO}} = \frac{{OC}}{{NO}}$

$\widehat {MOB} = \widehat {CON}$ (hai góc đối đỉnh)

=> $\Delta BOC$ ∽ $\Delta CNO$ (cạnh-góc-cạnh)

d) Xét tam giác $ABC$ , ta có:

$\begin{array}{l}\frac{{AC}}{{BC}} = \frac{{12}}{{15}} = \frac{4}{5}\\\frac{{AM}}{{MB}} = \frac{4}{5}\\ = > \frac{{AC}}{{BC}} = \frac{{AM}}{{MB}} = \frac{4}{5}\end{array}$

=> $CM$ là tia phân giác của tam giác $ABC$ .

Lại có:

$\widehat {NCM} = \widehat {MCB}$ (do CM là tia phân giác)

Mà $\widehat {NCM} = \widehat {MBN}$ (do $\Delta BMO$ ∽ $\Delta CNO$ )

Suy ra $\widehat {MCB} = \widehat {MBN}$

Mà $\widehat {MCB} = \widehat {MNB}$ (do $\Delta BOC$ ∽ $\Delta CNO$ )

Suy ra $\widehat {MBN} = \widehat {MNB}$

Vậy tam giác $MBN$ là tam giác cân tại $M$ .