Giải bài 6 trang 127 vở thực hành Toán 9 tập 2
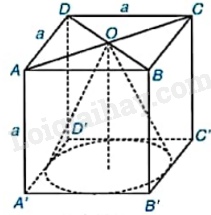
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A’B’C’D’.
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A’B’C’D’.
Phương pháp giải - Xem chi tiết
+ Hình nón có chiều cao \(h = a\), bán kính đáy \(R = \frac{{A'B'}}{2} = \frac{a}{2}\).
+ Thể tích hình nón chiều cao h, bán kính R là: \(V = \frac{1}{3}\pi {R^2}h\).
Lời giải chi tiết
\(R = \frac{a}{2}\); \(h = a\).
Thể tích của hình nón đó là:
\(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {\left( {\frac{a}{2}} \right)^2}a = \frac{{{a^3}\pi }}{{12}}\).
Cùng chủ đề:
Giải bài 6 trang 127 vở thực hành Toán 9 tập 2