Giải bài 6 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S. ABCD có SA vuông góc với mặt phẳng (ABCD) và \(SA = a\sqrt 3 \), đáy ABCD là hình thang vuông tại A và B có \(AB = a,AD = 3a,BC = a\).
Đề bài
Cho hình chóp S. ABCD có SA vuông góc với mặt phẳng (ABCD) và \(SA = a\sqrt 3 \), đáy ABCD là hình thang vuông tại A và B có \(AB = a,AD = 3a,BC = a\). Tính thể tích khối chóp S.BCD theo a.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\)
Lời giải chi tiết
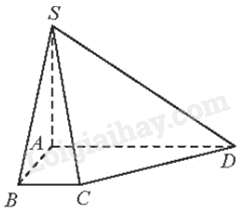
Diện tích tam giác BCD là:
\({S_{BCD}} \) \( = {S_{ABCD}} - {S_{ABD}} \) \( = \frac{{AB\left( {AD + BC} \right)}}{2} - \frac{1}{2}AB.AD \) \( = \frac{{AB.BC}}{2} \) \( = \frac{{{a^2}}}{2}\)
Thể tích khối chóp S.BCD là: \(V = \frac{1}{3}.SA.{S_{BCD}} = \frac{1}{3}.a\sqrt 3 .\frac{{{a^2}}}{2} = \frac{{{a^3}\sqrt 3 }}{6}\)
Cùng chủ đề:
Giải bài 6 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2