Giải bài 6 trang 87 SGK Toán 10 tập 1 – Chân trời sáng tạo
Gọi O là tâm hình lục giác đều ABCDEF.
Đề bài
Gọi O là tâm hình lục giác đều ABCDEF.
a) Tìm các vectơ khác vectơ →0 và cùng hướng với vectơ →OA.
b) Tìm các vectơ bằng vectơ →AB.
Phương pháp giải - Xem chi tiết
a)
Bước 1: Xác định các cạnh song song hoặc trùng với cạnh OA
Bước 2: Chỉ ra các vectơ cùng hướng với vectơ →OA
b)
Bước 1: Xác định các cạnh song song hoặc trùng cạnh AB
Bước 2: Chỉ ra các vectơ có cùng hướng với vectơ →AB
Bước 3: Trong đó, kết luận các vectơ có độ dài bằng cạnh AB
Lời giải chi tiết
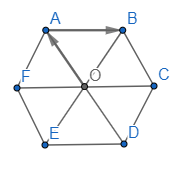
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ →0 và cùng hướng với vectơ →OA là : →DO,→DA,→CB,→EF
b) Ta có: OA=OB=OC=OD=OE=FO và AB // FC // ED
Suy ra các vectơ bằng vectơ →AB là →FO,→OC,→ED
Cùng chủ đề:
Giải bài 6 trang 87 SGK Toán 10 tập 1 – Chân trời sáng tạo