Giải bài 7. 21 trang 34 sách bài tập toán 11 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O$, cạnh bằng $a$, góc $BAD$ bằng ${60^ \circ }$. Kẻ $OH$ vuông góc với $SC$ tại $H$. Biết $SA \bot \left( {ABCD} \right)$ và $SA = \frac{{a\sqrt 6 }}{2}$. Chứng minh rằng:

a) $\left( {SBD} \right) \bot \left( {SAC} \right)$;

b) $\left( {SBC} \right) \bot \left( {BDH} \right)$;

c) $\left( {SBC} \right) \bot \left( {SCD} \right)$.

Lời giải chi tiết

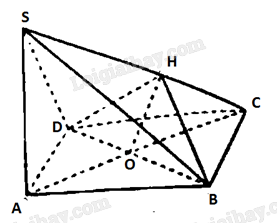
a) Ta có $SA \bot \left( {ABCD} \right)$ nên $SA \bot BD$ mà $BD \bot AC$, do đó $BD \bot \left( {SAC} \right)$.

Vì mặt phẳng $\left( {SBD} \right)$ chứa $BD$ nên $\left( {SBD} \right) \bot \left( {SAC} \right)$.

b) Ta có $BD \bot \left( {SAC} \right)$ nên $BD \bot SC$ mà $SC \bot OH$, do đó $SC \bot \left( {BDH} \right)$.

Vì mặt phẳng $\left( {SBC} \right)$ chứa $SC$ nên $\left( {SBC} \right) \bot \left( {BDH} \right)$.

c) Ta có: $SC = \sqrt {S{A^2} + A{C^2}}  = \frac{{3a\sqrt 2 }}{2}$

Vì $\Delta CHO$ và $\Delta CAS$ đồng dạng nên $\frac{{HO}}{{AS}} = \frac{{CO}}{{CS}}$, suy ra $HO = \frac{{CO \cdot AS}}{{CS}} = \frac{a}{2} = \frac{{BD}}{2}$.

Do đó, tam giác $BDH$ vuông tại $H$, suy ra $\widehat {BHD} = {90^ \circ }$.

Ta lại có $BH \bot SC,DH \bot SC$ nên $\left( {SBC} \right) \bot \left( {SCD} \right)$.