Giải bài 7. 22 trang 34 sách bài tập toán 11 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho hình chóp đều $S.ABCD$ có tất cả các cạnh bằng $a$. Tính côsin góc giữa hai mặt phẳng sau:

a) Mặt phẳng $\left( {SAB} \right)$ và mặt phẳng $\left( {ABCD} \right)$;

b) Mặt phẳng $\left( {SAB} \right)$ và mặt phẳng $\left( {SBC} \right)$.

Lời giải chi tiết

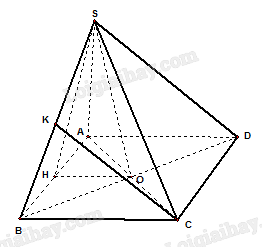
a) Gọi $O$ là giao điểm của $AC$ và $BD$.

Khi đó $SO \bot \left( {ABCD} \right)$ nên $SO \bot AB$,

Kẻ $OH \bot AB$ tại $H$ thì $AB \bot \left( {SOH} \right)$, suy ra $AB \bot SH$.

Do đó, góc giữa hai mặt phằng $\left( {SAB} \right)$ và $\left( {ABCD} \right)$ bằng góc giữa hai đường thẳng $SH$ vả $HO$, mà $\left( {SH,HO} \right) = \widehat {SHO}$ nên góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {ABCD} \right)$ bằng $\widehat {SHO}$.

Ta tính được ${\rm{OH}} = \frac{a}{2},{\rm{SH}} = \frac{{a\sqrt 3 }}{2}$, suy ra ${\rm{cos}}\widehat {SHO} = \frac{{{\rm{OH}}}}{{{\rm{SH}}}} = \frac{{\sqrt 3 }}{3}$.

b) Gọi $K$ là trung điểm của $SB$. Khi đó $AK \bot SB,CK \bot SB$, suy ra góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SBC} \right)$ bằng góc giữa hai đường thẳng $AK$ và $CK$.

Ta có $AK = CK = \frac{{a\sqrt 3 }}{2},AC = a\sqrt 2$.

Áp dụng định lí côsin trong tam giác ACK, ta có:

${\rm{cos}}\widehat {AKC} = \frac{{A{K^2} + C{K^2} - A{C^2}}}{{2 \cdot AK \cdot CK}} = \frac{{ - 1}}{3}$, suy ra ${\rm{cos}}\left( {AK,CK} \right) =  - {\rm{cos}}\widehat {AKC} = \frac{1}{3}$.

Vậy côsin góc giữa hai mặt phả̉ng $\left( {SAB} \right)$ và $\left( {SBC} \right)$ bằng $\frac{1}{3}$.