Giải bài 7.27 trang 37 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tính theo \(a\) khoảng cách
Đề bài
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tính theo \(a\) khoảng cách
a) Giữa hai đường thẳng \(AB\) và \(C'D'\).
b) Giữa đường thẳng \(AC\) và \(\left( {A'B'C'D'} \right)\).
c) Từ điểm \(A\) đường thẳng \(B'D'\).
d) Giữa hai đường thẳng \(AC\) và \(B'D'\).
Phương pháp giải - Xem chi tiết
a)
Bước 1: Xác định đường vuông góc chung hai đường thẳng
Bước 2: Tính độ dài đoạn vuông góc chung hai đường thẳng
b) Vì \(AC\parallel \left( {A'B'C'D'} \right)\) nên \(d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA'\).
c) Gọi \(O'\) là giao điểm của \(A'C'\) và \(B'D'\) ta có \(AO' \bot B'D'\), theo định lý Pythagore áp dụng cho tam giác \(AA'O'\) vuông tại \(A'\) thì \(AO' = \frac{{a\sqrt 6 }}{2}\).
Do đó, \(d\left( {A,B'D'} \right) = AO'\).
d) Ta có \(d\left( {AC,B'D'} \right) = d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA'\).
Lời giải chi tiết
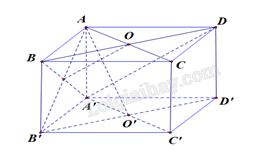
a) Vì \(BC'\) vuông góc với cả hai đường thẳng \(AB\)và \(C'D'\) nên \(d\left( {AB,C'D'} \right) = BC' = a\sqrt 2 \).
b) Vì \(AC\parallel \left( {A'B'C'D'} \right)\) nên \(d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA' = a\).
c) Gọi \(O'\) là giao điểm của \(A'C'\) và \(B'D'\) ta có \(AO' \bot B'D'\), theo định lý Pythagore áp dụng cho tam giác \(AA'O'\) vuông tại \(A'\) thì \(AO' = \frac{{a\sqrt 6 }}{2}\). Do đó, \(d\left( {A,B'D'} \right) = AO' = \frac{{a\sqrt 6 }}{2}\).
d) Ta có \(d\left( {AC,B'D'} \right) = d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA' = a\).