Giải bài 7.25 trang 35 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\)
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), tam giác \(SAD\) đều và nằm trong mặt phẳng vuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi \(H,M\) lần lượt là trung điểm của các cạnh \(AD\) và \(AB\).
a) Tính côsin của góc giữa đường thẳng \(SC\) và mặt đáy \(\left( {ABCD} \right)\).
b) Chứng minh rằng \(\left( {SMD} \right) \bot \left( {SHC} \right)\).
Phương pháp giải - Xem chi tiết
Áp dụng tính chất:
- Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng và vuông góc với giao tyến cũng vuông góc với mặt phẳng kia.
\(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\a \subset \left( P \right)\\b = \left( P \right) \cap \left( Q \right)\\a \bot b\end{array} \right. \Rightarrow a \bot \left( Q \right)\)
Ta có \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SH \bot AD\) nên \(SH \bot \left( {ABCD} \right)\),
Xác định hình chiếu của đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\)
Tính góc giữa hai đường thẳng \({\rm{SC}}\) và hình chiếu của nó rồi kết luận
Để chứng minh \(\left( {SDM} \right) \bot \left( {SCH} \right)\) sử dụng tính chất \(DM \bot CH,DM \bot SH\)
Lời giải chi tiết
a) Ta có \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SH \bot AD\) nên \(SH \bot \left( {ABCD} \right)\), suy ra góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng góc giữa hai đường thẳng \({\rm{SC}}\) và \({\rm{CH}}\), mà \(\left( {{\rm{SC}},{\rm{CH}}} \right) = \widehat {{\rm{SCH}}}\), ta tính được \(SH = \frac{{a\sqrt 3 }}{2},HC = \frac{{a\sqrt 5 }}{2}\) và \(SC = a\sqrt 2 \).
Do đó \({\rm{cos}}\widehat {SHC} = \frac{{HC}}{{SC}} = \frac{{\sqrt {10} }}{4}\).
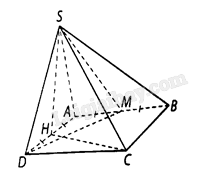
b) Ta có \(DM \bot CH,DM \bot SH\) nên \(DM \bot \left( {SCH} \right)\). Hơn nữa, mặt phẳng (SDM) chứa đường thẳng \(DM\) nên \(\left( {SDM} \right) \bot \left( {SCH} \right)\).