Giải bài 7.29 trang 38 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\)
Đề bài
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), góc \(ABC\) bằng \({60^ \circ }\), biết tam giác \(SBC\) đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng \(\left( {ABC} \right)\). Tính theo a khoảng cách:
a) Từ điểm \(S\) đến mặt phẳng \(\left( {ABC} \right)\).
b) Từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
c) Giữa hai đường thẳng \(AB\) và \(SC\).
Phương pháp giải - Xem chi tiết
a) Tính khoảng cách từ điểm \(S\) đến mặt phẳng \(\left( {ABC} \right)\).
Bước 1: Kẻ \(SH\) vuông góc với \(BC\) tại \(H\)
Do \(\left( {SBC} \right) \bot \left( {ABC} \right) \Rightarrow SH \bot \left( {ABC} \right)\)
\( \Rightarrow d\left( {S,\left( {ABC} \right)} \right) = SH\)
Bước 2: Tính \(SH\)
b) Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
Bước 1: Tính khoảng cách từ \(H\) đến mặt phẳng \(\left( {SAC} \right)\).
Bước 2: Nhận xét \(H\) là trung điểm của \(BC\) nên \(d\left( {B,\left( {SAC} \right)} \right) = 2d\left( {H,\left( {SAC} \right)} \right)\)c) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(SC\).
Bước 1: Dựng hình bình hành \(ABMC\), chứng minh được \(ABMC\) là hình chữ nhật.
Khi đó \(AB//\left( {SCM} \right)\) và mặt phẳng \(\left( {SMC} \right)\) chứa \(SC\) nên
\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCM} \right)} \right) = d\left( {B,\left( {SCM} \right)} \right) = 2d\left( {H,\left( {SCM} \right)} \right){\rm{.\;}}\)
Bước 2: Tính \(\left( {H,\left( {SCM} \right)} \right) \Rightarrow \)\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCM} \right)} \right) = 2d\left( {H,\left( {SCM} \right)} \right){\rm{.\;}}\)
Lời giải chi tiết
a) Kẻ \(SH\) vuông góc với \(BC\) tại \(H\) thì \(SH \bot \left( {ABC} \right)\), suy ra \(d\left( {S,\left( {ABC} \right)} \right) = SH = \frac{{a\sqrt 3 }}{2}\)
b) Kẻ HK vuông góc với \(AC\) tại \(K,HQ\) vuông góc với \(SK\) tại \(Q\) thì \(d\left( {H,\left( {SAC} \right)} \right) = HQ\).
Ta có: \(AB = \frac{a}{2},HK = \frac{a}{4}\) và tam giác \(SHK\) vuông tại \(H\), đường cao \(HQ\) nên \(HQ = \frac{{SH \cdot HK}}{{SK}} = \frac{{a\sqrt {39} }}{{26}}\).
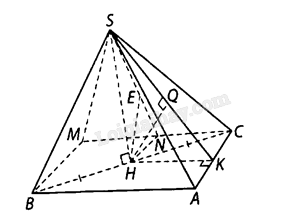
Lại có \(H\) là trung điểm của \(BC\) nên \(d\left( {B,\left( {SAC} \right)} \right) = 2d\left( {H,\left( {SAC} \right)} \right) = \frac{{a\sqrt {39} }}{{13}}\).
c) Dựng hình bình hành \(ABMC\), chứng minh được \(ABMC\) là hình chữ nhật.
Khi đó \(AB//\left( {SCM} \right)\) và mặt phẳng \(\left( {SMC} \right)\) chứa \(SC\) nên
\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCM} \right)} \right) = d\left( {B,\left( {SCM} \right)} \right) = 2d\left( {H,\left( {SCM} \right)} \right){\rm{.\;}}\)
Kẻ \(HN\) vuông góc với \(CM\) tại \(N,HE\) vuông góc với \(SN\) tại \(N\) thì \(HE \bot \left( {SCM} \right)\), suy ra \(d\left( {H,\left( {SCM} \right)} \right) = HE\).
Ta có: \(HN = \frac{{BM}}{2} = \frac{{a\sqrt 3 }}{4}\), tam giác SHN vuông tại \(H\), đường cao \(HE\) nên \(HE = \frac{{SH \cdot HN}}{{SN}} = \frac{{a\sqrt {15} }}{{10}}\).
Vậy \(d\left( {AB,SC} \right) = \frac{{a\sqrt {15} }}{5}\).