Giải bài 7. 34 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho khối chóp đều $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $a$, góc giữa mặt phẳng $\left( {SCD} \right)$ và mặt phẳng $\left( {ABCD} \right)$ bằng $60^\circ$. Tính theo $a$ thể tích khối chóp $S.ABCD$.

Lời giải chi tiết

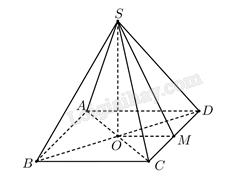
Gọi $O$ là giao điểm của $AC$ và $BD$, ta có $SO$ vuông góc với mặt đáy $\left( {ABCD} \right)$. Kẻ $OM$ vuông góc với $CD$ tại $M$ thì $SM$ cũng vuông góc với $CD$ nên góc giữa hai mặt phẳng $\left( {SCD} \right)$ và $\left( {ABCD} \right)$ bằng góc giữa hai đường thẳng $SM$ và $OM$, mà $\left( {SM,OM} \right) = \widehat {SMO} = 60^\circ$. Ta có: $OM = \frac{a}{2};$$SO = OM \cdot {\rm{tan}}\widehat {SMO} = \frac{{a\sqrt 3 }}{2}$. Vậy ${V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{1}{3} \cdot {a^2} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{{6}}$.