Giải bài 7.39 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\) và \(\widehat {BAC} = {60^ \circ }\)
Đề bài
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\) và \(\widehat {BAC} = {60^ \circ }\), biết diện tích các tam giác \(ABC,SAB\) và \(SAC\) lần lượt là \(3\sqrt 3 ;9;12\). Tính thể tích khối chóp \(S.ABC\).
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính thể tích khối chóp: \({\rm{S}} = \frac{1}{3}{\rm{Bh}}\).
Trong đó: \({\rm{B}}\) là diện tích đa giác đáy
h là đường cao của hình chóp
Bước 1:
Đặt \(SA = a,AB = b,AC = c\).
Khi đó \({V_{S.ABC}} = \frac{1}{3} \cdot {S_{ABC}} \cdot SA = \frac{1}{3} \cdot \frac{1}{2} \cdot bc \cdot {\rm{sin}}{60^ \circ } \cdot a = \frac{{abc\sqrt 3 }}{{12}}\)
Bước 2:
Theo đề bài, ta có: \({S_{ABC}} = \frac{1}{2}bc \cdot {\rm{sin}}{60^ \circ } = 3\sqrt 3 \), suy ra \(bc\).
\({S_{SAB}} = \frac{{ab}}{2} = 9\), suy ra \(ab = \),
\({S_{SAC}} = \frac{{ac}}{2}\) suy ra \(ac\).
Nhân \(ab.bc.ca = {\left( {abc} \right)^2} \Rightarrow abc \Rightarrow {V_{S.ABC}}\)
Lời giải chi tiết
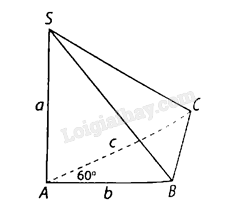
Đặt \(SA = a,AB = b,AC = c\).
Khi đó \({V_{S.ABC}} = \frac{1}{3} \cdot {S_{ABC}} \cdot SA = \frac{1}{3} \cdot \frac{1}{2} \cdot bc \cdot {\rm{sin}}{60^ \circ } \cdot a = \frac{{abc\sqrt 3 }}{{12}}\)
Theo đề bài, ta có: \({S_{ABC}} = \frac{1}{2}bc \cdot {\rm{sin}}{60^ \circ } = 3\sqrt 3 \), suy ra \(bc = 12\).
\({S_{SAB}} = \frac{{ab}}{2} = 9\), suy ra \(ab = 18;{S_{SAC}} = \frac{{ac}}{2} = 12\), suy ra \(ac = 24\).
Do đó \({(abc)^2} = 12 \cdot 18 \cdot 24 = {72^2}\), hay \(abc = 72\).
Vậy \({V_{S.ABC}} = 6\sqrt 3 \).