Giải bài 7.37 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình chóp có đáy \(ABCD\) là hình thoi tâm \(O\), biết \(SO \bot \left( {ABCD} \right)\)
Đề bài
Cho hình chóp có đáy \(ABCD\) là hình thoi tâm \(O\), biết \(SO \bot \left( {ABCD} \right)\), \(AC = 2a\sqrt 3 ,BD = 2a\) và khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 3 }}{2}\). Tính theo \(a\) thể tích khối chóp \(S.ABCD\).
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính thể tích khối chóp: \({\rm{S}} = \frac{1}{3}{\rm{Bh}}\).
Trong đó: \({\rm{B}}\) là diện tích đa giác đáy
h là đường cao của hình chóp
Bước 1: Tính chiều cao \(SO\) của hình chóp
Phân tích: \(d\left( {A,\left( {SBC} \right)} \right) = 2 \cdot d\left( {O,\left( {SBC} \right)} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right)\)
Dựng hình
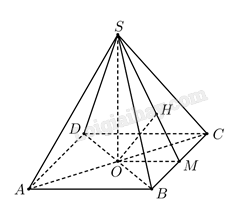
Khoảng cách từ \(d\left( {O,\left( {SBC} \right)} \right) = OH\)
Xét tam giác \(SOM\) vuông tại \(O\), đường cao \(OH\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{S^2}}}\), suy ra \(SO\).
Bước 2: Tính diện tích đáy \(ABCD\)
Bước 3: Tính thể tích khối chóp \(S.ABCD\): \({V_{S \cdot ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO\)
Lời giải chi tiết
Kẻ \(OM\) vuông góc với \(BC\) tại \(M,OH\) vuông góc với \(SM\) tại \(H\), ta chứng minh được \(OH \bot \left( {SBC} \right)\). Vì \(O\) là trung điểm của \(AC\) nên\(d\left( {A,\left( {SBC} \right)} \right) = 2 \cdot d\left( {O,\left( {SBC} \right)} \right) = 2 \cdot OH = \frac{{a\sqrt 3 }}{2}\),
suy ra \({\rm{OH}} = \frac{{{\rm{a}}\sqrt 3 }}{4}\).
Tam giác \(OBC\) vuông tại \(O\), có \(OB = a,OC = a\sqrt 3 \)
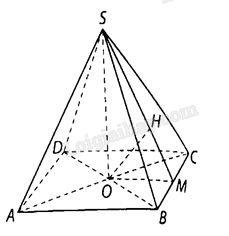
và đường cao \(OM\) nên \(OM = \frac{{OB \cdot OC}}{{BC}} = \frac{{a\sqrt 3 }}{2}\).
Tam giác \(SOM\) vuông tại \(O\), đường cao \(OH\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{S^2}}}\), suy ra \(SO = \frac{a}{2}\).
Vậy \({V_{S \cdot ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{1}{3} \cdot \frac{1}{2} \cdot 2a\sqrt 3 \cdot 2a \cdot \frac{a}{2} = \frac{{{a^3}\sqrt 3 }}{3}\).