Giải bài 7 trang 22 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Một nhà máy có ba bộ phận cắt, may, đóng gói để sản phẩm ba loại sản phẩm: áo thun, áo sơ mi, áo khoác. Thời gian (tính bằng phút) của mỗi bộ phận để sản xuất 10 cái áo mỗi loại được thể hiện trong bảng sau:
Đề bài
Một nhà máy có ba bộ phận cắt, may, đóng gói để sản phẩm ba loại sản phẩm: áo thun, áo sơ mi, áo khoác. Thời gian (tính bằng phút) của mỗi bộ phận để sản xuất 10 cái áo mỗi loại được thể hiện trong bảng sau:
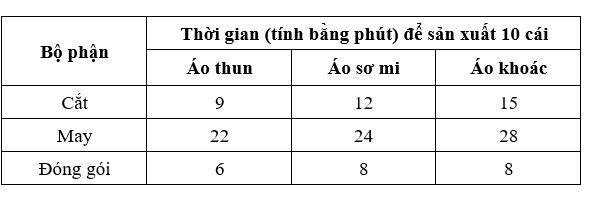
Các bộ phận cắt, may và đóng gói có tối đa 80, 160 và 48 giờ lao động tương ứng mỗi ngày. Hãy lập kế hoạch sản xuất để nhà máy hoạt động hết công suất.
Phương pháp giải - Xem chi tiết
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết
Giả sử x, y, z là số áo thun áo sơ mi, áo khoác mà nhà máy sản xuất khi hoạt động hết công suất.
Tổng số giờ cắt là 80 giờ = 4800 phút nên \(9.\frac{x}{{10}} + 12.\frac{y}{{10}} + 15.\frac{z}{{10}} = 4800\)
Tổng số giờ may là 160 giờ = 9600 phút nên \(22.\frac{x}{{10}} + 24.\frac{y}{{10}} + 28.\frac{z}{{10}} = 9600\)
Tổng số giờ cắt là 48 giờ = 2880 phút nên \(6.\frac{x}{{10}} + 8.\frac{y}{{10}} + 8.\frac{z}{{10}} = 2880\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn:
\(\left\{ \begin{array}{l}9.\frac{x}{{10}} + 12.\frac{y}{{10}} + 15.\frac{z}{{10}} = 4800\\22.\frac{x}{{10}} + 24.\frac{y}{{10}} + 28.\frac{z}{{10}} = 9600\\6.\frac{x}{{10}} + 8.\frac{y}{{10}} + 8.\frac{z}{{10}} = 2880\end{array} \right.\)
Dùng máy tính cầm tay, ta suy ra \(x = 800,y = 1400,z = 1600\)
Vậy để hoạt động hết công suất nhà máy cần sản xuất 800 cái áo thun, 1400 áo sơ mi và 1600 áo khoác.