Giải bài 6 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Một sao chổi A chuyển động theo quỹ đạo có dạng một parabol (P) nhận tâm Mặt Trời là tiêu điểm. Cho biết khoảng cách ngắn nhất giữa sao chổi A và tâm Mặt Trời là khoảng 112 km.

a) Viết phương trình chính tắc của parabol (P)

b) Tính khoảng cách giữa sao chổi A và tâm Mặt Trời khi sao chổi nằm trên đường thẳng đi qua tiêu điểm và vuông góc với trục đối xứng của (P).

Lời giải chi tiết

a) Gọi PTCT của parabol là ${y^2} = 2px$

Với $M(x;y)$ bất kì nằm trên parabol, ta có: $MF = x + \frac{p}{2} \ge \frac{p}{2}$ (do $x \ge 0$)

Vì khoảng cách ngắn nhất giữa sao chổi A và tâm Mặt Trời là khoảng 112 km nên $\frac{p}{2} = 112 \Leftrightarrow p = 224$

$\Rightarrow$ Phương trình chính tắc của (P) là: ${y^2} = 448x$

b)

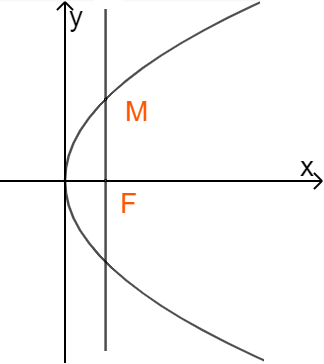
Gọi $M(x;y)$ là vị trí sao chổi A, nằm trên đường thẳng đi qua tiêu điểm và vuông góc với trục đối xứng của (P).

Parabol (P) có tiêu điểm $F(112;0)$ $\Rightarrow M(112;y)$

$MF = \left| {{y_M}} \right| = \sqrt {2.224.112}  = 224$

Vậy khoảng cách là 224 km.