Giải bài 76 trang 37 sách bài tập toán 12 - Cánh diều
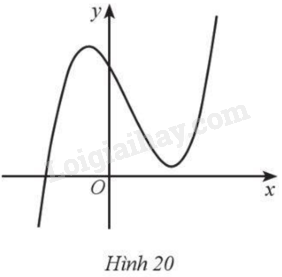
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số (y = a{x^3} + b{x^2} + cx + dleft( {a ne 0} right)) có đồ thị là đường cong ở Hình 20. a) (a > 0). b) Đồ thị cắt trục tung tại điểm có tung độ dương. c) Đồ thị hàm số có hai điểm cực trị nằm cùng phía với trục tung. d) (b < 0).
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\) có đồ thị là đường cong ở Hình 20. a) \(a > 0\). b) Đồ thị cắt trục tung tại điểm có tung độ dương. c) Đồ thị hàm số có hai điểm cực trị nằm cùng phía với trục tung. d) \(b < 0\).
Phương pháp giải - Xem chi tiết
‒ Dựa vào hình dáng của đồ thị hàm số.
‒ Xét giao điểm của đồ thị hàm số với các trục toạ độ.
‒ Xét các điểm cực trị của hàm số.
Lời giải chi tiết
• Căn cứ hình dáng của đồ thị hàm số, ta có: \(a > 0\). Vậy a) đúng.
• Đồ thị cắt trục tung tại điểm \(\left( {0;d} \right)\) nằm phía trên trục hoành nên điểm đó có tung độ dương. Vậy b) đúng.
• Đồ thị hàm số có hai điểm cực trị nằm ở hai phía trục tung. Vậy c) sai.
• Trung điểm của đoạn nối hai điểm cực trị \({x_1},{x_2}\) nằm bên phải trục tung nên \({x_1} + {x_2} = - \frac{{2b}}{{3{\rm{a}}}} > 0 \Leftrightarrow \frac{{2b}}{{3{\rm{a}}}} < 0\). Do \(a > 0\) nên \(b < 0\). Vậy d) đúng.
a) Đ.
b) Đ.
c) S.
d) Đ.