Giải bài 8 trang 103 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn tâm O bán kính OA và đường tròn tâm O' đường kính OA. a) Xét vị trí tương đối của hai đường tròn (O) và (O'). b) Dây AD của đường tròn (O) cắt đường tròn (O’) tại C. Chứng minh AC = CD.
Đề bài
Cho đường tròn tâm O bán kính OA và đường tròn tâm O' đường kính OA.
a) Xét vị trí tương đối của hai đường tròn (O) và (O').
b) Dây AD của đường tròn (O) cắt đường tròn (O’) tại C. Chứng minh AC = CD.
Phương pháp giải - Xem chi tiết
a) Chỉ ra \(OO' = OA - O'A\)
b) Bước 1: Chứng minh \(OC \bot DC\) (do \(O'C = \frac{1}{2}AO\) nên tam giác OAC vuông tại C).
Bước 2: OC là đường cao đồng thời là đường trug tuyến trong tam giác cân OAD.
Lời giải chi tiết
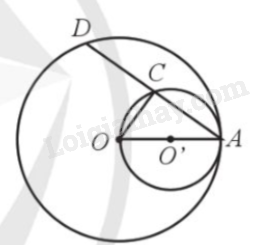
a) Vì đường tròn tâm O' đường kính OA nên \(OO' = O'A = \frac{{OA}}{2}\)
Do đó \(OO' = OA - O'A\) nên 2 đường tròn (O) và (O) tiếp xúc trong tại A.
b) Xét tam giác OAC có: \(CO' = OO' = AO'( = r)\) suy ra \(O'C = \frac{1}{2}AO\) nên tam giác OAC vuông tại C. Do đó \(OC \bot DC\).
Xét tam giác DOA cân tại O (\(OD = OA = R\)) có đường cao OC (do \(OC \bot DC\)) đồng thời là đường trung tuyến nên CD = CA.