Giải bài 8 trang 107 sách bài tập toán 9 - Cánh diều tập 2
Ở Hình 9 biết ABCDEF là lục giác đều, chứng minh rằng lục giác MNPQRS cũng là lục giác đều.
Đề bài
Ở Hình 9 biết ABCDEF là lục giác đều, chứng minh rằng lục giác MNPQRS cũng là lục giác đều.
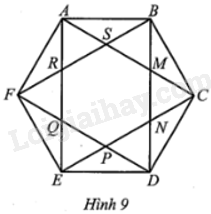
Phương pháp giải - Xem chi tiết
Dựa vào đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lời giải chi tiết
Lục giác ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA và
\(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAF} = \widehat {FAB}\).
Ta cũng có tổng 6 góc của lục giác đều ABCDEF bằng tổng các góc của hai tứ giác ABCD và AFED, tức là bằng 2.360° = 720°.
Do đó:
\(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAF} = \widehat {FAB} = \frac{{{{720}^o}}}{6} = {120^o}.\)
Xét ∆AFB cân tại A (do AB = AF) ta có:
\(\widehat {ABF} = \widehat {AFB} = \frac{{{{180}^o} - \widehat {FAB}}}{2} = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\)
Hay \(\widehat {ABS} = \widehat {AFR} = {30^o}\).
Tương tự, đối với ∆ABC cân tại B ta có: \(\widehat {BAC} = \widehat {BCA} = {30^o}\) hay \(\widehat {BAS} = {30^o}\).
Do đó ta có \(\widehat {ABS} = \widehat {BAS} = {30^o}\). Nên ∆ABS cân tại S.
Suy ra \(\widehat {ASB} = {180^o} - 2\widehat {BAS} = {180^o} - {2.30^o} = {120^o}\).
Khi đó, \(\widehat {RSM} = \widehat {ASB} = {120^o}\)(đối đỉnh).
Chứng minh tương tự, ta được:
\(\widehat {RSM} = \widehat {SMN} = \widehat {MNP} = \widehat {NPQ} = \widehat {PQR} = \widehat {QRS} = {120^o}\). (1)
Ta có: \(\widehat {BSA} + \widehat {BSM} = {180^o}\) (kề bù)
Suy ra \(\widehat {BSM} = {180^o} - \widehat {BSA} = {180^o} - {120^o} = {60^o}\).
Ta cũng có: \(\widehat {BMS} = {180^o} - \widehat {BMC} = {180^o} - {120^o} = {60^o}\).
Do đó ∆BSM là tam giác cân, lại có \(\widehat {BSM} = {60^o}\)nên ∆BSM là tam giác đều.
Suy ra SB = SM = BM.
Chứng minh tương tự ta có ∆SAR là tam giác đều nên SA = SR = AR.
Do ∆ABS cân tại S nên SA = SB.
Khi đó, RS = SM.
Chứng minh tương tự, ta được:
RS = SM = MN = NP = PQ = QR. (2)
Từ (1) và (2) suy ra lục giác MNPQRS là lục giác đều.