Giải bài 8 trang 61 sách bài tập toán 12 - Cánh diều — Không quảng cáo

Đề bài

Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hình chóp tứ giác đều \(S.ABCD\) có độ dài tất cả các cạnh đều bằng \(a\) (Hình 10). a) Tứ giác \(ABCD\) là hình vuông. b) Tam giác \(SAC\) vuông cân tại \(S\). c) \(\left( {\overrightarrow {SA} ,\overrightarrow {AC} } \right) = {45^ \circ }\). d) \(\overrightarrow {SA} .\overrightarrow {AC} = - {a^2}\).

Lời giải chi tiết

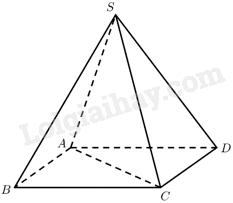
\(S.ABCD\) là chóp tứ giác đều nên tứ giác \(ABCD\) là hình vuông. Vậy a) đúng.

\(ABCD\) là hình vuông nên \(AC = \sqrt {A{B^2} + B{C^2}}  = a\sqrt 2 \).

Tam giác \(SAC\) có: \(S{A^2} + S{C^2} = 2{{\rm{a}}^2} = A{C^2}\).

Vậy tam giác \(SAC\) vuông cân tại \(S\). Vậy b) đúng.

\(\begin{array}{l}\cos \left( {\overrightarrow {SA} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {SA} .\overrightarrow {AC} }}{{\left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{ - \overrightarrow {AS} .\overrightarrow {AC} }}{{\left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{ - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AS} ,\overrightarrow {AC} } \right)}}{{\left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AC} } \right|}}\\ &  = \frac{{ - a.a\sqrt 2 .\cos \widehat {SAC}}}{{a.a\sqrt 2 }} = \frac{{ - a.a\sqrt 2 .\cos {{45}^ \circ }}}{{a.a\sqrt 2 }} =  - \frac{{\sqrt 2 }}{2}\end{array}\)

\( \Rightarrow \left( {\overrightarrow {SA} ,\overrightarrow {AC} } \right) = {135^ \circ }\). Vậy c) sai.

\(\overrightarrow{SA}.\overrightarrow{AC}=-\overrightarrow{AS}.\overrightarrow{AC}=-\left| \overrightarrow{AS} \right|.\left| \overrightarrow{AC} \right|.\cos \left( \overrightarrow{AS},\overrightarrow{AC} \right)=-a.a\sqrt{2}.\cos \widehat{SAC}=-a.a\sqrt{2}.\cos {{45}^{\circ }}=-{{a}^{2}}\)

Vậy d) đúng.

a) Đ

b) Đ

c) S

d) Đ