Giải bài 8 trang 75 vở thực hành Toán 9
Cho tam giác ABC vuông tại A, biết (AB = 6cm,AC = 8cm). a) Tính tanB, cạnh BC, sinB, góc B (làm tròn đến độ). b) Kẻ đường cao AH. Tính AH, BH, cos (widehat {BAH}).
Đề bài
Cho tam giác ABC vuông tại A, biết \(AB = 6cm,AC = 8cm\).
a) Tính tanB, cạnh BC, sinB, góc B (làm tròn đến độ).
b) Kẻ đường cao AH. Tính AH, BH, cos \(\widehat {BAH}\).
Phương pháp giải - Xem chi tiết
a) + Tam giác ABC có: \(\tan B = \frac{{AC}}{{AB}}\).
+ Áp dụng Pythagore vào tam giác ABC tính được BC.
+ \(\sin B = \frac{{AC}}{{BC}}\)
b) Trong tam giác vuông ABH có:
+ \(\sin B = \frac{{AH}}{{AB}}\) từ đó tính được AH; \(\tan B = \frac{{AH}}{{BH}}\) từ đó tính được BH.
+ \(\cos \widehat {BAH} = \sin B = \frac{4}{5}\) (vì \(\widehat {BAH}\) và góc B là hai góc phụ nhau).
Lời giải chi tiết
(H.4.9)
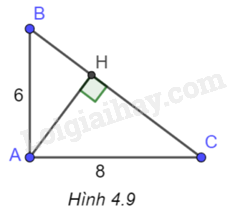
a) Trong tam giác ABC có \(\tan B = \frac{{AC}}{{AB}} = \frac{8}{6} = \frac{4}{3}\).
Theo định lí Pythagore, ta có \(B{C^2} = A{C^2} + A{B^2} = {8^2} + {6^2} = 100\)
\(BC = \sqrt {100} = 10cm\)
Ta có \(\sin B = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5}\), từ đó suy ra \(\widehat B \approx {53^o}\)
b) Trong tam giác vuông ABH có:
\(\sin B = \frac{{AH}}{{AB}}\), suy ra \(AH = AB.\sin B = 6.\frac{4}{5} = \frac{{24}}{5}\left( {cm} \right)\)
\(\tan B = \frac{{AH}}{{BH}}\), suy ra \(BH = \frac{{AH}}{{\tan B}} = \frac{{24}}{5}:\frac{4}{3} = \frac{{18}}{5}\left( {cm} \right)\)
\(\cos \widehat {BAH} = \sin B = \frac{4}{5}\) (vì \(\widehat {BAH}\) và góc B là hai góc phụ nhau).