Giải bài 8 trang 90 sách bài tập toán 8 - Cánh diều — Không quảng cáo

Đề bài

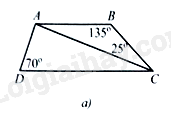
a)     Cho tứ giác $ABCD$ có $AB//CD,\widehat B = 135^\circ ,\widehat D = 70^\circ ,\widehat {ACB} = 25^\circ$ (Hình 8a). Tính số đo góc $DAC$.

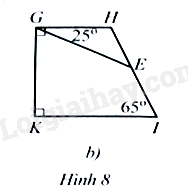
b)    Cho tứ giác $GHIK$ có $\widehat {KGH} = \widehat K = 90^\circ ,\widehat I = 65^\circ$. Trên $HI$ lấy điểm $E$ sao cho $\widehat {EGH} = 25^\circ$ (Hình 8b). Tính số đo góc $GEI$.

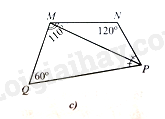
c)     Cho tứ giác $MNPQ$ có $PM$ là tia phân giác của góc $NPQ,\widehat {QMN} = 110^\circ ,\widehat N = 120^\circ ,\widehat Q = 60^\circ$ (Hình 8c). Tính các số đo góc $NPM,MPQ,QMP$.

Lời giải chi tiết

a)     Trong tam giác $ABC$, ta có: $\widehat {BAC} = 180^\circ  - \left( {\widehat B + \widehat {BCA}} \right) = 20^\circ$

Do $AB//CD$ nên $\widehat {ACD} = \widehat {BAC} = 20^\circ$ (hai góc so le trong)

Trong tam giác $ACD$, ta có: $\widehat {DAC} = 180^\circ  - \left( {\widehat {ACD} + \widehat D} \right) = 90^\circ$

b)    Trong tứ giác $GHIK$, ta có: $\widehat H = 360^\circ  - \left( {\widehat {KGH} + \widehat I + \widehat K} \right) = 115^\circ$

Trong tam giác $GHE$, ta có: $\widehat {HEG} = 180^\circ  - \left( {\widehat {EGH} + \widehat H} \right) = 40^\circ$

Vậy $\widehat {GEI} = 180^\circ  - \widehat {HEG} = 140^\circ$

c)     Trong tứ giác $MNPQ$, ta có: $\widehat {NPQ} = 360^\circ  - \left( {\widehat {QMN} + \widehat N + \widehat Q} \right) = 70^\circ$

Do $PM$ là tia phân giác của góc $NPQ$ nên $\widehat {NPM} = \widehat {MPQ} = \frac{{\widehat {NPQ}}}{2} = 35^\circ$

Trong tam giác $MPQ$, ta có: $\widehat {QMP} = 180^\circ  - \left( {\widehat {MPQ} + \widehat Q} \right) = 85^\circ$