Giải bài 9.29 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
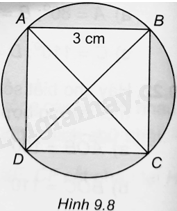
Cho hình vuông ABCD có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.8. Tính tổng diện tích của bốn hình viên phân được giới hạn bởi các cạnh hình vuông (phần tô đậm trong hình).
Đề bài
Cho hình vuông ABCD có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.8. Tính tổng diện tích của bốn hình viên phân được giới hạn bởi các cạnh hình vuông (phần tô đậm trong hình).
Phương pháp giải - Xem chi tiết
+ Tính diện tích hình vuông ABCD.
+ Áp dụng định lí Pythagore vào tam giác ABC vuông tại B tính được AC.
+ Đường tròn ngoại tiếp hình vuông ABCD có bán kính là: \(R = \frac{{AC}}{2}\).
+ Diện tích hình tròn ngoại tiếp hình vuông ABCD là: \({S_2} = \pi .{R^2}\).
Tổng diện tích bốn hình viên phân giới hạn bởi các cạnh hình vuông là: \(S = {S_2} - {S_1}\).
Lời giải chi tiết
Diện tích hình vuông ABCD là: \({S_1} = {3^2} = 9\left( {c{m^2}} \right)\).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có: \(A{C^2} = A{B^2} + B{C^2} = 18\) nên \(AC = 3\sqrt 2 cm\)
Đường tròn ngoại tiếp hình vuông ABCD có bán kính là: \(R = \frac{{AC}}{2} = \frac{{3\sqrt 2 }}{2}\left( {cm} \right)\).
Diện tích hình tròn ngoại tiếp hình vuông ABCD là: \({S_2} = \pi .{R^2} = \frac{9}{2}\pi \left( {c{m^2}} \right)\).
Tổng diện tích bốn hình viên phân giới hạn bởi các cạnh hình vuông là: \(S = {S_2} - {S_1} = \frac{9}{2}\pi - 9\left( {c{m^2}} \right)\).