Giải bài 9.31 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho hình chữ nhật ABCD nội tiếp đường tròn (O) với AB=3cm; AD=4cm. Vẽ một hình vuông nội tiếp (O). Tính diện tích của hình vuông đó.
Đề bài
Cho hình chữ nhật ABCD nội tiếp đường tròn (O) với AB=3cm; AD=4cm. Vẽ một hình vuông nội tiếp (O). Tính diện tích của hình vuông đó.
Phương pháp giải - Xem chi tiết
+ Áp dụng định lí Pythagore vào tam giác ABD vuông tại A tính được BD.
+ Đường tròn (O) có tâm O là trung điểm BD và bán kính \(R = \frac{{BD}}{2}\).
+ Hình vuông nội tiếp (O) có cạnh bằng a, có đường chéo \(\sqrt {{a^2} + {a^2}} = a\sqrt 2 \).
+ Đường tròn (O) ngoại tiếp hình vuông nên \(R = \frac{{a\sqrt 2 }}{2}\), từ đó tính được a.
+ Hình vuông có diện tích là: \(S = {a^2}\).
Lời giải chi tiết
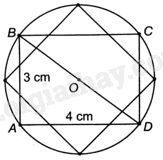
Áp dụng định lí Pythagore vào tam giác ABD vuông tại A có: \(B{D^2} = A{B^2} + A{D^2} = 25\) nên \(BD = 5cm\).
Đường tròn (O) có tâm O là trung điểm BD và bán kính \(R = \frac{{BD}}{2} = 2,5cm\).
Hình vuông nội tiếp (O) có cạnh bằng a, có đường chéo \(\sqrt {{a^2} + {a^2}} = a\sqrt 2 \).
Đường tròn (O) ngoại tiếp hình vuông nên \(R = \frac{{a\sqrt 2 }}{2}\), suy ra \(a = \frac{{2R}}{{\sqrt 2 }} = \frac{{5\sqrt 2 }}{2}cm\).
Hình vuông có diện tích là: \(S = {a^2} = 12,5c{m^2}\).