Giải bài 9. 36 trang 60 sách bài tập toán 9 - Kết nối tri thức tập 2 — Không quảng cáo

Đề bài

Cho lục giác đều ABCDEF nội tiếp một đường tròn (O). Chứng minh rằng điểm O cách đều tất cả các cạnh của lục giác đều.

Lời giải chi tiết

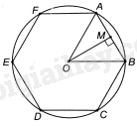
Gọi a là độ dài cạnh của lục giác đều ABCDEF. Gọi M là trung điểm của AB. Vì tam giác OAB đều nên $OM \bot AB$ và OM là tia phân giác của góc AOB.

Suy ra: $OM = OA.\sin \widehat {OAM} = a.\sin {60^o} = \frac{{a\sqrt 3 }}{2}$. Do đó, khoảng cách từ O đến AB bằng $\frac{{a\sqrt 3 }}{2}$.

Chứng minh tương tự ta có: khoảng cách từ O đến tất cả các cạnh của lục giác đều bằng $\frac{{a\sqrt 3 }}{2}$.