Giải bài 9 trang 24 Chuyên đề học tập Toán 11 Cánh diều
Quan sát Hình 43 và chỉ ra:
Đề bài
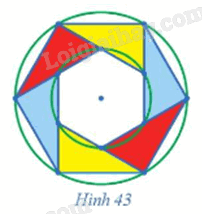
Quan sát Hình 43 và chỉ ra:
a) Một phép dời hình biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
b) Một phép dời hình biến mỗi tam giác được tô màu xanh thành tam giác được tô màu vàng.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức:
- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.
- Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay
Lời giải chi tiết
Đặt các điểm như hình vẽ.
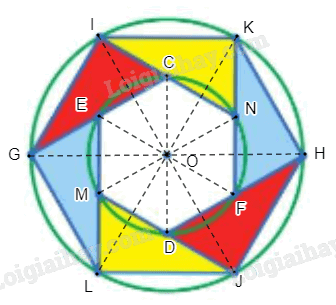
a) Ta thấy đường tròn nhỏ tâm O có các đường kính CD, EF, MN nên O là trung điểm của CD, EF, MN. Đường tròn lớn tâm O có các đường kính GH, LK, IJ nên O là trung điểm của GH, LK, IJ.
Do đó, ta có phép đối xứng tâm O biến các điểm I, K, N, H, F, D, J tương ứng thành các điểm J, L, M, G, E, C, I.
Từ đó suy ra phép đối xứng tâm O biến các tam giác IKN, KHF, HJD tương ứng thành các tam giác JLM, LGE, GIC hay chính là phép đối xứng tâm O biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
b) Ta có \(\widehat {KOJ} = \frac{{360^\circ }}{3} = 120^\circ \) và \(OK{\rm{ }} = {\rm{ }}OJ\;\) nên ta có phép quay tâm O với góc quay – 120° biến điểm K thành điểm J.
Ta có \(\widehat {HOL} = 120^\circ \) và \(OH{\rm{ }} = {\rm{ }}OL\) nên ta có phép quay tâm O với góc quay – 120° biến điểm H thành điểm L.
Ta có \(\widehat {FOM} = 120^\circ \) và \(OF{\rm{ }} = {\rm{ }}OM\) nên ta có phép quay tâm O với góc quay – 120° biến điểm F thành điểm M.
Do đó, ta có phép quay tâm O với góc quay – 120° biến tam giác KHF thành tam giác JLM.
Tương tự, ta có phép quay tâm O với góc quay – 120° biến tam giác LGE thành tam giác IKN.
Như vậy, phép quay tâm O với góc quay – 120° biến mỗi tam giác được tô màu xanh thành tam giác được tô màu vàng.