Giải bài 8 trang 33 Chuyên đề học tập Toán 11 Cánh diều — Không quảng cáo

Đề bài

Cho hai đường tròn (O ₁ ; R) và (O ₂ ; 2R) tiếp xúc ngoài với nhau tại điểm A. Tìm phép vị tự biến đường tròn (O ₁ ; R) thành đường tròn $({O_2};{\rm{ }}2R).$

Lời giải chi tiết

Hai đường tròn (O ₁ ; R) và (O ₂ ; 2R) tiếp xúc ngoài với nhau tại điểm A và đường tròn tâm O ₂ có bán kính gấp 2 lần đường tròn tâm O ₁ .

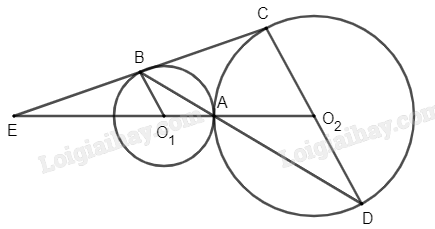
- Trên đường tròn $({O_1};{\rm{ }}R)$ lấy điểm B bất kì.

- Trên đường tròn $({O_2};{\rm{ }}2R)$ dựng đường kính CD // O _1­­ B.

- BC cắt O ₁ O ₂ tại E.

+) Ta có: O ₁ B // CO ₂ nên theo định lí Thales có $\frac{{E{O_2}}}{{E{O_1}}} = \frac{{{O_2}C}}{{{O_1}B}} = \frac{{2R}}{R} = 2$.

Suy ra $\overrightarrow {E{O_2}}  = 2\overrightarrow {E{O_1}}$ nên ta có phép vị tự tâm E, tỉ số 2 biến điểm O ₁ thành điểm O ₂ .

Như vậy, phép vị tự tâm E, tỉ số 2 biến đường tròn $({O_1};{\rm{ }}R)$ thành đường tròn $({O_2};{\rm{ }}2R).$

+) Nối B với D, ta chứng minh được BD cắt O ₁ O ₂ tại điểm tiếp xúc A của hai đường tròn.

Ta có:  $\frac{{A{O_2}}}{{A{O_1}}} = \frac{{2R}}{R} = 2$ và A nằm giữa hai điểm O ₁ và O ₂ nên $\overrightarrow {A{O_2}}  =  - 2\overrightarrow {A{O_1}}$. Do đó, ta có phép vị tự tâm A, tỉ số – 2 biến điểm O ₁ thành điểm O ₂ .

Như vậy, phép vị tự tâm A, tỉ số – 2 biến đường tròn (O ₁ ; R) thành đường tròn $({O_2};{\rm{ }}2R)$.

Vậy có 2 phép vị tự biến đường tròn $({O_1};{\rm{ }}R)$ thành đường tròn $({O_2};{\rm{ }}2R)$.