Giải bài tập 1.33 trang 46 SGK Toán 12 tập 1 - Cùng khám phá
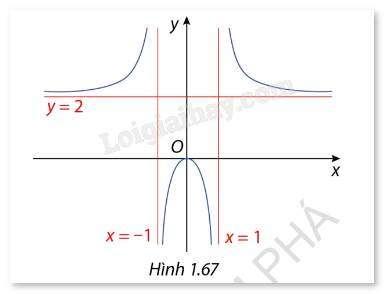
Cho hàm số \(y = \frac{{2{x^2}}}{{{x^2} - 1}}\) có đồ thị là đường cong như Hình 1.67. Xác định các đường tiệm cận đứng, tiệm cận ngang và tiệm cận xiên (nếu có) của đồ thị hàm số đã cho.
Đề bài
Cho hàm số \(y = \frac{{2{x^2}}}{{{x^2} - 1}}\) có đồ thị là đường cong như Hình 1.67. Xác định các đường tiệm cận đứng, tiệm cận ngang và tiệm cận xiên (nếu có) của đồ thị hàm số đã cho.
Phương pháp giải - Xem chi tiết
Nhìn vào đồ thị và tìm đường thẳng thoả mãn các điều kiện sau:
- Tiệm cận đứng: Có dạng x = a, giá trị của hàm số sẽ tiến tới vô cực khi x tiến dần đến a.
- Tiệm cận ngang: Có dạng y = k, đồ thị của hàm số tiến dần đến k khi x tiến ra vô cực.
- Tiệm cận xiên: Có dạng y = ax+b, không tồn tại song song với tiệm cận ngang.
Lời giải chi tiết
- Tiệm cận đứng: \(x = \pm 1\)
- Tiệm cận ngang: \(y = 2\)
- Tiệm cận xiên: Không tồn tại vì hàm số đã có tiệm cận ngang.
Cùng chủ đề:
Giải bài tập 1. 33 trang 46 SGK Toán 12 tập 1 - Cùng khám phá