Giải bài tập 1.44 trang 44 SGK Toán 12 tập 1 - Kết nối tri thức
Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức: \(\frac{1}{p} + \frac{1}{q} = \frac{1}{f}\). a) Viết công thức tính \(q = g\left( p \right)\) như một hàm số của biến \(p \in \left( {f; + \infty } \right)\). b) Tính các giới hạn \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right),\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right)\) và giải thích ý nghĩa các kết quả này. Lập bảng bi
Đề bài
Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức: \(\frac{1}{p} + \frac{1}{q} = \frac{1}{f}\).
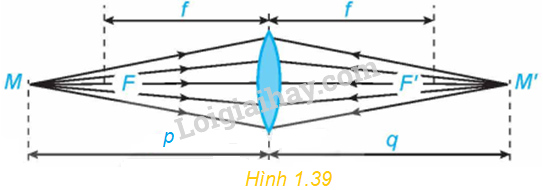a) Viết công thức tính \(q = g\left( p \right)\) như một hàm số của biến \(p \in \left( {f; + \infty } \right)\).
b) Tính các giới hạn \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right),\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right)\) và giải thích ý nghĩa các kết quả này.
Lập bảng biến thiên của hàm số \(q = g\left( p \right)\) trên khoảng \(\left( {f; + \infty } \right)\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính giới hạn của hàm số để tính.
Sử dụng kiến thức về lập bảng biến thiên của hàm số để lập bảng biến thiên: Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
Lời giải chi tiết
a) Ta có: \(\frac{1}{p} + \frac{1}{q} = \frac{1}{f} \Rightarrow q = \frac{{pf}}{{p - f}}\). Do đó, \(q = g\left( p \right) = \frac{{pf}}{{p - f}}\) với \(p \in \left( {f; + \infty } \right)\).
b) \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right) = \mathop {\lim }\limits_{p \to + \infty } \frac{{pf}}{{p - f}} = \mathop {\lim }\limits_{p \to + \infty } \frac{f}{{1 - \frac{f}{p}}} = f,\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right) = \mathop {\lim }\limits_{p \to {f^ + }} \frac{{pf}}{{p - f}} = + \infty \)
Ý nghĩa của \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right) = f\): Khoảng cách từ vật đến thấu kính tiến ra vô cùng thì khoảng cách từ ảnh đến thấu kính xấp xỉ tiêu cự.
Ý nghĩa của \(\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right) = + \infty \): Khoảng cách từ vật đến thấu kính tiến gần về tiêu cự f thì khoảng cách từ ảnh đến thấu kính là càng lớn.
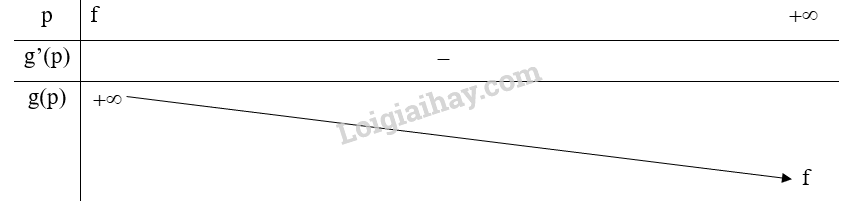
c) Ta có: \(q' = g'\left( p \right) = \frac{{ - {f^2}}}{{{{\left( {p - f} \right)}^2}}} < 0\;\forall p \in \left( {f; + \infty } \right)\) nên hàm số nghịch biến trên \(\left( {f; + \infty } \right)\).
Bảng biến thiên:
