Giải bài tập 1.49 trang 49 SGK Toán 12 tập 1 - Cùng khám phá
Đường cong trong Hìhh 1.71 là đồ thị của hàm số nào sau đây? A. \(y = \frac{{2x + 1}}{{2x - 2}}\). B. \(y = \frac{{x + 1}}{{x - 1}}\). C. \(y = \frac{{ - x}}{{1 - x}}\). D. \(y = \frac{{x - 1}}{{x + 1}}\).
Đề bài
Đường cong trong Hìhh 1.71 là đồ thị của hàm số nào sau đây?
A. \(y = \frac{{2x + 1}}{{2x - 2}}\)
B. \(y = \frac{{x + 1}}{{x - 1}}\)
C. \(y = \frac{{ - x}}{{1 - x}}\)
D. \(y = \frac{{x - 1}}{{x + 1}}\)
Phương pháp giải - Xem chi tiết
Đồ thị của hàm số phân thức bậc nhất \(y = \frac{{ax + b}}{{cx + d}}\) thường có một số đặc điểm như sau:
- Tiệm cận đứng xảy ra tại các giá trị của 𝑥 mà mẫu số bằng 0.
- Tiệm cận ngang là đường thẳng mà hàm số tiến gần đến khi 𝑥→±∞.
- Tiệm cận xiên là đường thẳng mà hàm số tiến gần đến khi 𝑥→±∞ nếu không có tiệm cận ngang.
- Cắt trục hoành tại điểm \(\left( { - \frac{b}{a};0} \right)\).
- Cắt trục tung tại điểm \(\left( {0;\frac{b}{d}} \right)\).
Lời giải chi tiết
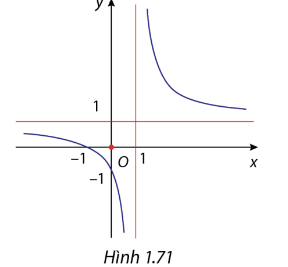
Nhìn vào hình 1.71 ta thấy đồ thị hàm số có:
- Một tiệm cận đứng là \(x = 1\), suy ra mẫu số của hàm sẽ bằng 0 khi \(x = 1\) → Loại D.
- Một tiệm cận ngang là \(y = 1\), suy ra khi 𝑥→±∞ thì giới hạn của hàm số sẽ bằng 1 → Loại C.
- Đồ thị hàm số cắt trục tung tại (0;−1), suy ra \(\frac{b}{d} = - 1\) → Loại A.
Đáp án đúng là B.