Giải bài tập 10 trang 22 SGK Toán 9 tập 2 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hàm số $y = a{x^2}\left( {a \ne 0} \right)$.

a) Tìm a, biết đồ thị của hàm số đi qua điểm M(2;2).

b) Vẽ đồ thị (P) của hàm số với a vừa tìm được.

c) Tìm các điểm thuộc đồ thị (P) trên có tung độ y = 8.

Lời giải chi tiết

a) Thay x = 2; y = 2 vào hàm số $y = a{x^2}\left( {a \ne 0} \right)$, ta được:

2 = a.2 ² suy ra a = $\frac{1}{2}$.

b) Theo phần a ta vẽ đồ thị hàm số $y = \frac{1}{2}{x^2}$.

Bảng giá trị:

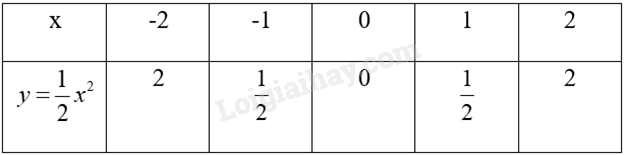
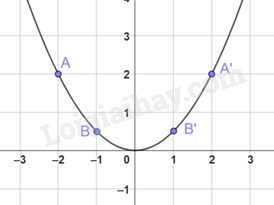
Trên mặt phẳng tọa độ, lấy các điểm A(-2;-2), B(-1; $\frac{1}{2}$), O(0;0), B’(1; $\frac{1}{2}$), A’(2;2)

Đồ thị hàm số $y = \frac{1}{2}{x^2}$là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như dưới đây.

c) Thay y = 8 vào $y = \frac{1}{2}{x^2}$, ta được:

$\begin{array}{l}8 = \frac{1}{2}{x^2}\\{x^2} = 16\\x =  \pm 4\end{array}$

Vậy có 2 điểm thuộc đồ thị là: $\left( {4;8} \right)$ và $\left( { - 4;8} \right)$.