Giải bài tập 2 trang 110 SGK Toán 9 tập 1 - Cánh diều
Cho đường tròn (left( O right)) và dây (AB). Điểm (M) nằm ngoài đường tròn (left( O right)) thỏa mãn điểm (B) nằm trong góc (MAO) và (widehat {MAB} = frac{1}{2}widehat {AOB}). Chứng minh đường thẳng (MA) là tiếp tuyến của đường tròn (left( O right)).
Đề bài
Cho đường tròn \(\left( O \right)\) và dây \(AB\). Điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) thỏa mãn điểm \(B\) nằm trong góc \(MAO\) và \(\widehat {MAB} = \frac{1}{2}\widehat {AOB}\). Chứng minh đường thẳng \(MA\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Phương pháp giải - Xem chi tiết
Dựa vào tính chất tiếp tuyến để chứng minh.
Lời giải chi tiết
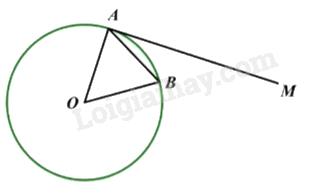
Ta có: \(OA = OB = R\) nên tam giác \(OAB\) cân tại \(O\) suy ra \(\widehat {OAB} = \widehat {OBA}\).
Xét tam giác \(OAB\) cân tại \(O\) có:
\(\begin{array}{l}\widehat {OAB} + \widehat {OBA} + \widehat {AOB} = 180^\circ \Rightarrow \widehat {OAB} + \widehat {OAB} + \widehat {AOB} = 180^\circ \\ \Rightarrow 2\widehat {OAB} = 180^\circ - \widehat {AOB} \Rightarrow \widehat {OAB} = 90^\circ - \frac{1}{2}\widehat {AOB}.\end{array}\)
Ta có: \(\widehat {OAM} = \widehat {OAB} + \widehat {BAM} = 90^\circ - \frac{1}{2}\widehat {AOB} + \frac{1}{2}\widehat {AOB} = 90^\circ .\)
Suy ra \(OA \bot AM\). Vậy \(MA\) là tiếp tuyến của đường tròn \(\left( O \right)\).