Giải bài tập 5. 23 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức — Không quảng cáo

Đề bài

Kim tự tháp Kheops ở Ai Cập có dạng hình chóp S. ABCD, có đáy là hình vuông với cạnh dài 230m, các cạnh bên bằng nhau và dài 219m (theo britannica.com ) (H.5.38). Tính góc giữa hai mặt phẳng (SAB) và (SBC).

Lời giải chi tiết

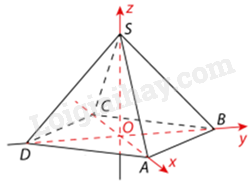
Gọi O là giao điểm của AC và BD, khi đó ta tính được $OA = OB = OC = OD = 115\sqrt 2$

Vì $SA = SB = SC = SD$ nên tam giác SAC và SBD là các tam giác cân tại S. Do đó, SO vừa là đường trung tuyến vừa là đường cao của các tam giác SAC và SBD. Do đó, $SO \bot AC,SO \bot BD$ nên $SO \bot \left( {ABCD} \right)$.

Tam giác SOA vuông tại O nên $SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {{{219}^2} - {{\left( {115\sqrt 2 } \right)}^2}}  = 7\sqrt {439}$

Chọn hệ trục tọa độ Oxyz có gốc tọa độ trùng với O như hình vẽ.

Khi đó, $S\left( {0;0;7\sqrt {439} } \right),A\left( {115\sqrt 2 ;0;0} \right);B\left( {0;115\sqrt 2 ;0} \right),C\left( { - 115\sqrt 2 ;0;0} \right)$

Suy ra: $\overrightarrow {SA} \left( {115\sqrt 2 ;0; - 7\sqrt {439} } \right),\overrightarrow {AB} \left( { - 115\sqrt 2 ;115\sqrt 2 ;0} \right) \Rightarrow \overrightarrow m  = \frac{1}{{115\sqrt 2 }}\overrightarrow {AB}  = \left( { - 1;1;0} \right)$,

$,\overrightarrow {SB} \left( {0;115\sqrt 2 ; - 7\sqrt {439} } \right)$, $\overrightarrow {BC} \left( { - 115\sqrt 2 ; - 115\sqrt 2 ;0} \right) \Rightarrow \overrightarrow v  = \frac{1}{{ - 115\sqrt 2 }}\overrightarrow {BC}  = \left( {1;1;0} \right)$

$\left[ {\overrightarrow {SA} ,\overrightarrow m } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 7\sqrt {439} }\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 7\sqrt {439} }&{115\sqrt 2 }\\0&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{115\sqrt 2 }&0\\{ - 1}&1\end{array}} \right|} \right)$$= \left( {7\sqrt {439} ;7\sqrt {439} ;115\sqrt 2 } \right)$

Mặt phẳng (SAB) nhận $\overrightarrow {{n_1}}  = \left[ {\overrightarrow {SA} ,\overrightarrow m } \right] = \left( {7\sqrt {439} ;7\sqrt {439} ;115\sqrt 2 } \right)$ làm vectơ pháp tuyến.

$\left[ {\overrightarrow {SB} ,\overrightarrow v } \right] = \left( {\left| {\begin{array}{*{20}{c}}{115\sqrt 2 }&{ - 7\sqrt {439} }\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 7\sqrt {439} }&0\\0&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{115\sqrt 2 }\\1&1\end{array}} \right|} \right)$$= \left( {7\sqrt {439} ; - 7\sqrt {439} ; - 115\sqrt 2 } \right)$

Mặt phẳng (SBC) nhận $\overrightarrow {{n_2}}  = \left[ {\overrightarrow {SB} ,\overrightarrow v } \right] = \left( {7\sqrt {439} ; - 7\sqrt {439} ; - 115\sqrt 2 } \right)$ làm vectơ pháp tuyến.

Ta có: $\left( {\left( {SAB} \right),\left( {SBC} \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|$

$= \frac{{\left| {{{\left( {7\sqrt {439} } \right)}^2} - {{\left( {7\sqrt {439} } \right)}^2} - {{\left( {115\sqrt 2 } \right)}^2}} \right|}}{{\sqrt {{{\left( {7\sqrt {439} } \right)}^2} + {{\left( {7\sqrt {439} } \right)}^2} + {{\left( {115\sqrt 2 } \right)}^2}} .\sqrt {{{\left( {7\sqrt {439} } \right)}^2} + {{\left( { - 7\sqrt {439} } \right)}^2} + {{\left( { - 115\sqrt 2 } \right)}^2}} }}$

$= \frac{{{{\left( {115\sqrt 2 } \right)}^2}}}{{69\;472}} = \frac{{13225}}{{34736}} \Rightarrow \left( {\left( {SAB} \right),\left( {SBC} \right)} \right) \approx 67,{6^o}$

Vậy góc giữa hai mặt phẳng (SAB) và (SBC) bằng $67,{6^o}$.