Giải bài tập 5 trang 102 SGK Toán 9 tập 1 - Chân trời sáng tạo
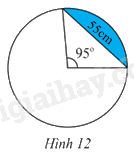
Tính diện tích hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung số đo là 95o. (Hình 12).
Đề bài
Tính diện tích hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung số đo là 95 o . (Hình 12).
Phương pháp giải - Xem chi tiết
- Tính diện tích tam giác OAB.
- Tính diện tích hình quạt tròn OamB.
- Tính diện tích hình viên phân AmB = diện tích hình quạt tròn OamB - diện tích tam giác OAB.
Lời giải chi tiết
Gọi các điểm như hình dưới:
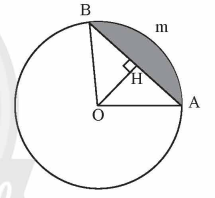
Gọi AmB là hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung có số đo $95^\circ$.
Vẽ $OH \perp AB$ tại $H$. Khi đó $H$ là trung điểm của $AB$.
Suy ra $AH = BH = \frac{AB}{2} = \frac{55}{2} = 27,5 \text{ (cm)}.$
Ta có $OA = OB = R$ nên $\Delta OAB$ cân tại $O$.
Mà $OH \perp AB$ nên $OH$ là tia phân giác của góc $AOB$, suy ra $\widehat {AOH} = \frac{\widehat {AOB}}{2} = \frac{95^\circ}{2} = 47,5^\circ.$
Áp dụng hệ thức giữa cạnh và góc trong $\Delta AOH$ vuông tại $H$, ta có:
$OH = AH \cdot \cot \widehat {AOH} = 27,5 \cdot \cot 47,5^\circ \approx 25,2 \text{ (cm)}; $
$OA = \frac{AH}{\sin \widehat {AOH}} = \frac{27,5}{\sin 47,5^\circ} \approx 37,3 \text{ (cm)}. $
Diện tích của tam giác $OAB$ là:
$S_{OAB} = \frac{1}{2} \cdot OH \cdot AB = \frac{1}{2} \cdot 25,2 \cdot 55 \approx 693 \text{ (cm}^2). \quad (1) $
Diện tích hình quạt tròn $OAmB$ là:
$S_{OAmB} = \frac{\pi R^2 n}{360} \approx \frac{\pi \cdot (37,3)^2 \cdot 95}{360} \approx 1153,42 \text{ (cm}^2). \quad (2) $
Từ $(1)$ và $(2)$ suy ra diện tích hình viên phân $AmB$ là:
$S_{AmB} = S_{OAmB} - S_{OAB} \approx 1153,42 - 693 \approx 460,42 \text{ (cm}^2). $