Giải bài tập 5 trang 66 SGK Toán 9 tập 1 - Cánh diều
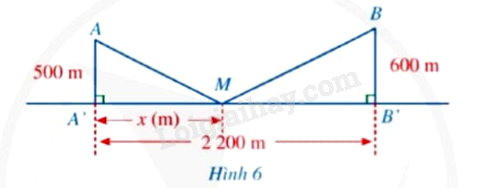
Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xác đó đến bờ sông lần lượt là (AA' = 500m,BB' = 600m) và người ta đo dược (A'B' = 2200m). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Giả sử vị trí của trạm cung cấp nước sạch đó là điểm M trên đoạn (A'B') với (MA' = xleft( m right)), (0 < x < 2200) (minh họa ở Hình 6). a. Hãy tính tổng khoảng cách (MA + MB) theo (x). b. Tính tổng khoảng cách (MA + MB) khi (x = 1200)
Đề bài
Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xác đó đến bờ sông lần lượt là \(AA' = 500m,BB' = 600m\) và người ta đo dược \(A'B' = 2200m\). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Giả sử vị trí của trạm cung cấp nước sạch đó là điểm M trên đoạn \(A'B'\) với \(MA' = x\left( m \right)\), \(0 < x < 2200\) (minh họa ở Hình 6) .
a. Hãy tính tổng khoảng cách \(MA + MB\) theo \(x\).
b. Tính tổng khoảng cách \(MA + MB\) khi \(x = 1200\) (làm tròn kết quả đến hàng đơn vị của mét).
Phương pháp giải - Xem chi tiết
Áp dụng định lí Py – ta – go và căn thức đế tính.
Lời giải chi tiết
a. Ta có: \(MB = 2200 - x\)
Áp dụng định lý Py – ta – go vào tam giác MAA’ ta có:
\(\begin{array}{l}M{A^2} = MA{'^2} + AA{'^2}\\M{A^2} = {x^2} + {500^2}\\MA = \sqrt {{x^2} + {{500}^2}} \end{array}\)
Áp dụng định lý Py – ta – go vào tam giác \(MBB'\) ta có:
\(\begin{array}{l}M{B^2} = BB{'^2} + MB{'^2} \Rightarrow M{B^2} = {600^2} + {\left( {2200 - x} \right)^2}\\MB = \sqrt {{600^2} + {\left( {2200 - x} \right)^2}} \end{array}\)
Vậy \(MA + MB = \sqrt {{x^2} + {{500}^2}} + \sqrt {{600^2} + {\left( {2200 - x} \right)^2}}. \)
b. Thay \(x = 1200\) vào biểu thức tính \(MA + MB\), ta được:
\(MA + MB = \sqrt {{{1200}^2} + {{500}^2}} + \sqrt {{600^2} + {\left( {2200 - 1200} \right)^2}} \\ = \sqrt {1440000 + 250000} + \sqrt {{600^2} + {1000^2}} \\ = \sqrt {1690000} + \sqrt {1360000} \\MA + MB \approx 2466\left( m \right).\)